这系列文章是慕课网《算法与数据结构》实战课程老师的讲授内容笔记整理,其中有很多动图都是我参考老师的动画演示自己制作的,并提供 JS(es6) 版的代码示例。代码仓库:📦 https://github.com/Mitscherlich/Play-with-Algorithms-JS
在前面的几节中我为大家介绍了四种经典的排序算法,尤其重点介绍了三种高级排序算法。而接下来这一小节将为大家介绍另一种数据结构:二分搜索树。二叉搜索树被广泛应用在解决查找问题上,其本质上还是一棵二叉树,这和前面我们已经学习过的最大堆有些类似,但又有一些本质上的不同。事实上,二叉树是计算机算法中应用非常广泛的的一种数据结构,不同类型的二叉树能很好的应用于各类问题。

查找问题
查找问题是计算机中非常重要的基础问题。查找问题看起来不难,但实际上应用非常广泛,例如各类搜索引擎的本质就是查找算法的应用。在介绍二叉搜索树之前,我们先来了解一下二分查找法。
二分查找法
二分查找(又称折半查找)只能应用在有序的数组上,因为我们处理有序数组比处理无序数组要方便得多。这也可以看出我们前面学习那么多排序算法的原因:很多时候排序算法都是作为其他算法的子过程来使用的。
假定一个数组有序数组,要查找元素值为
e,这是只需与数组中间的值 v 进行比较:
如果
e 正好等于 v,那么 v 显然就是我们要找的元素;否则,以 v 为界数组将分为 < v、v、> v 三部分:
如果元素
e 比 v 大(或小),那么只需在对应的部分重复这两步操作即可。二分搜索法的思想非常简单,事实上它在 1946 年就被首次提出; 然而第一个没有 bug 的二分查找法直到 1962 年才被实现。
// 二分查找法,在有序数组 arr 中,查找 target
// 如果找到 target, 返回相应的索引 index
// 如果没有找到 target, 返回 -1
Array.prototype.binarySearch = function (target) {
const array = this.slice()
const n = array.length
// 在 arr[l...r] 之中查找 target
let l = 0
let r = n - 1
while (l <= r) {
// let mid = Math.floor((l + r) / 2)
// 防止极端情况下的整形溢出,使用下面的逻辑求出 mid
const mid = l + Math.floor((r - l) / 2)
if (array[mid] === target) {
return mid
}
if (target < array[mid]) {
// 在 arr[l...mid] 之中查找 target
r = mid - 1
} else {
// 在 arr[mid...r] 之中查找 target
l = mid + 1
}
}
return -1
}使用递归实现二分查找法
由上面的过程不难看出,二分查找法也可以方便的通过递归来实现:
function binarySearch (array, l, r, target) {
if (l > r) {
return -1
}
// let mid = Math.floor((l + r) / 2)
// 防止极端情况下的整形溢出,使用下面的逻辑求出 mid
const mid = l + Math.floor((r - l) / 2)
if (array[mid] === target) {
return mid
} else if (target < array[mid]) {
// 在 arr[l...mid] 之中查找 target
return binarySearch(array, l, mid - 1, target)
} else {
// 在 arr[mid...r] 之中查找 target
return binarySearch(array, mid + 1, r, target)
}
}
Array.prototype.binarySearch = function (target) {
const array = this.slice()
const n = array.length
return binarySearch(array, 0, n - 1, target)
}floor 和 ceil
floor 和 ceil 也是数组中两个常用的操作。这里的 floor 和 ceil 和我们常用的 Math.floor 和 Math.ceil 有所不同,后者是求不大于一个数的最大整数和不小于一个数的最小整数,前者是找出目标元素在数组中的起始或末尾。
特殊地,如果一个元素不存在在数组中,则
floor 将找到小于目标的最大元素的末尾,而 ceil 将找到大于目标元素的最小元素的起始。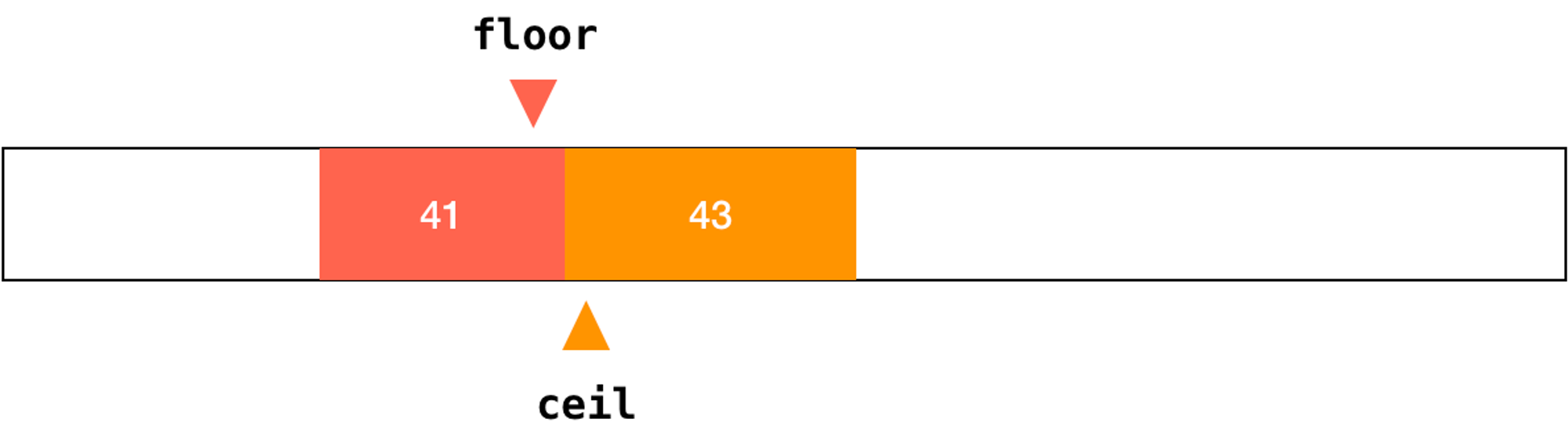
这两个过程也很容易通过修改现有的二分搜索过程来实现,这里就不做展开,有兴趣的同学可以到代码仓库找到对应的代码了解即可。
二分搜索树
接下来我们具体介绍并实现二分搜索树这种数据结构。当我们说到二分搜索树,通常和另一种数据结构联系起来,那就是查找表。查找表是一种以键值对形式存储数据的数据结构,通常,查找表有多种实现形式,如图展示了不同的实现形式的操作性能:
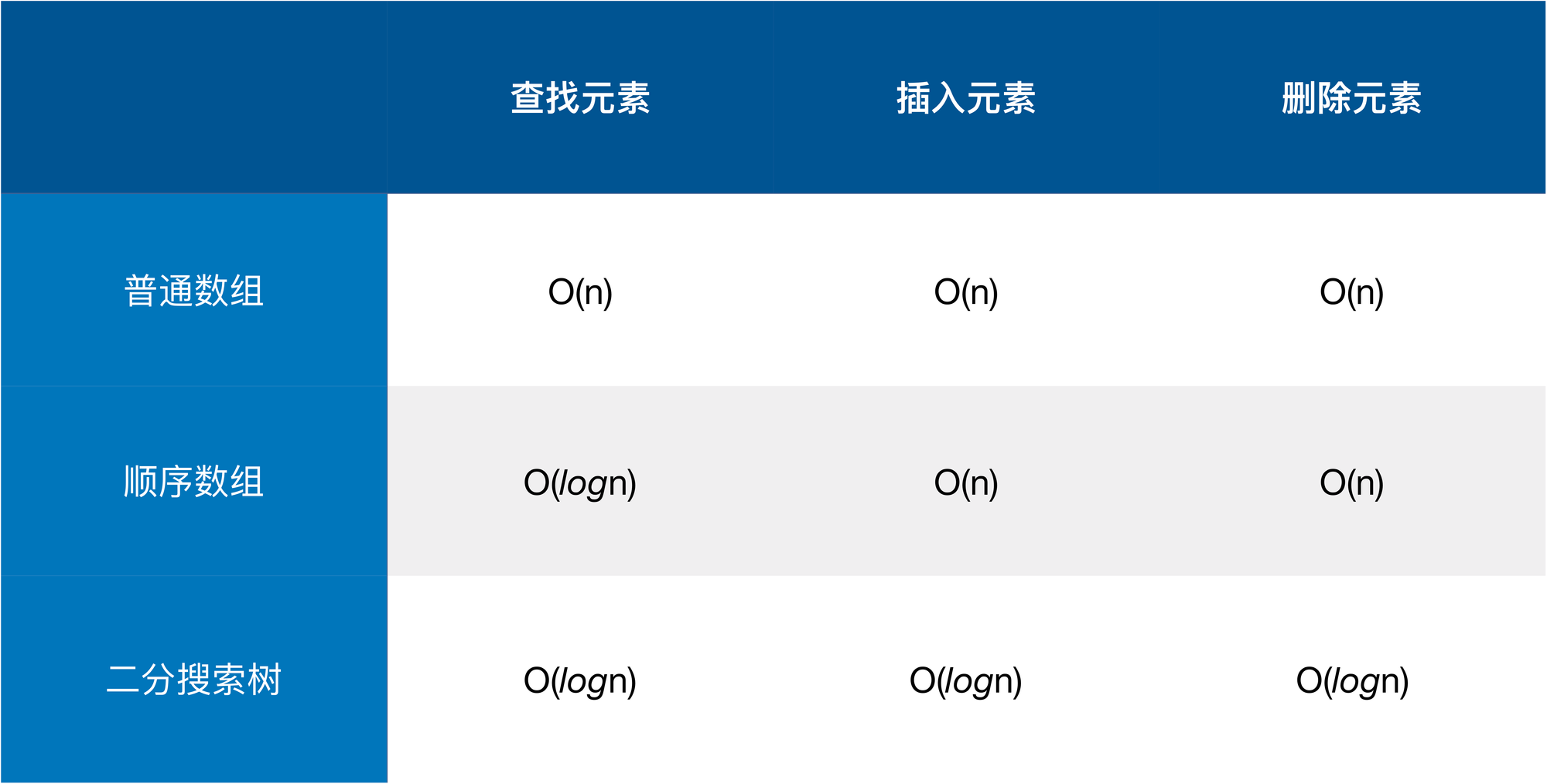
而我们其实主要就是使用二分搜索树来实现查找表。
二分搜索树的性质
二分搜索树本质上还是一科二叉树,同时又具有一些特殊的性质:
- 任意节点的左子树总是小于当前节点的值;
- 任意节点的右子树总是大于当前节点的值;
- 没有键值相等的节点。
显然,由于树的递归性质,那么只要一个节点有左(右)子树,那么它的左(右)肯定也是一棵二分搜索树。
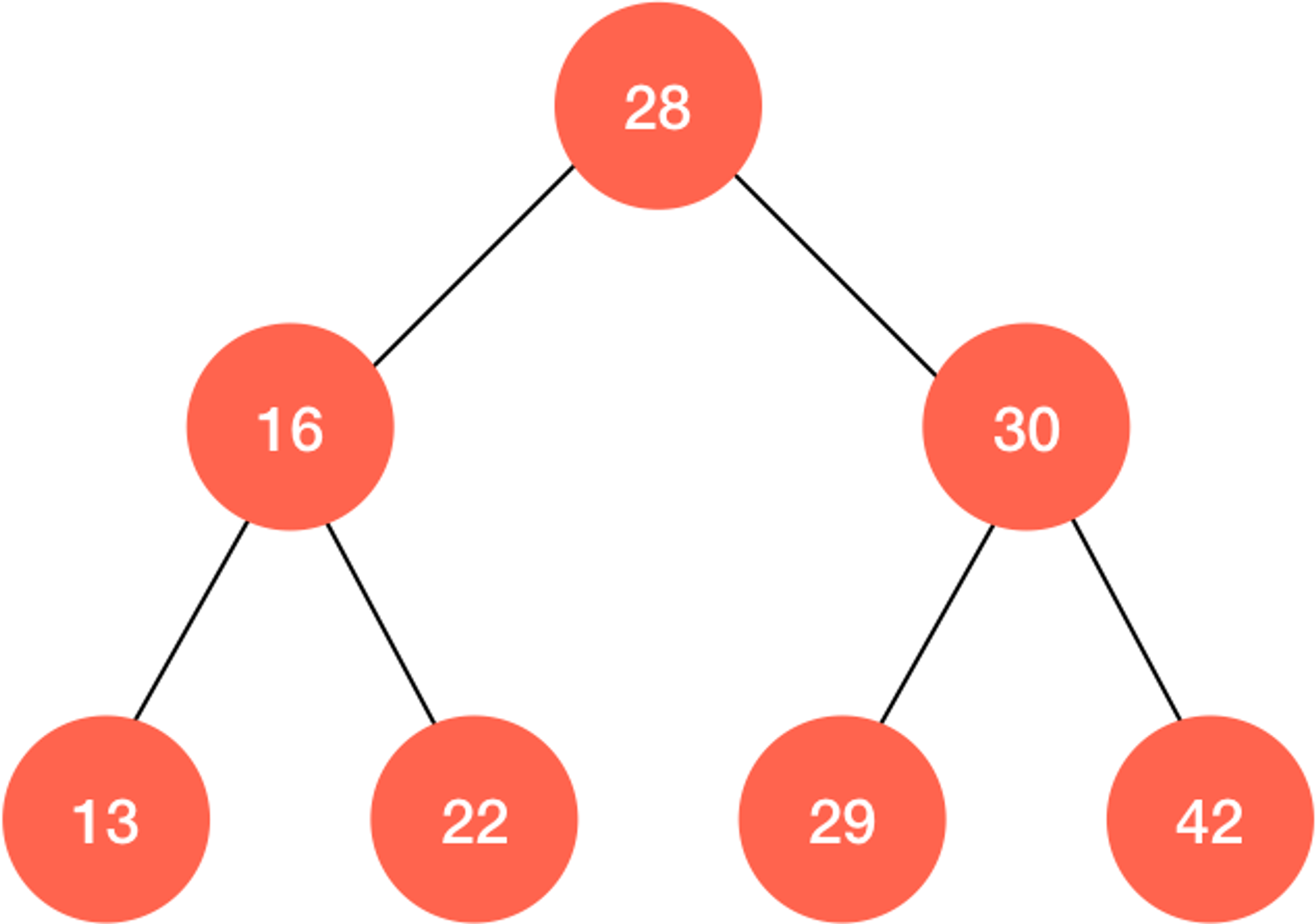
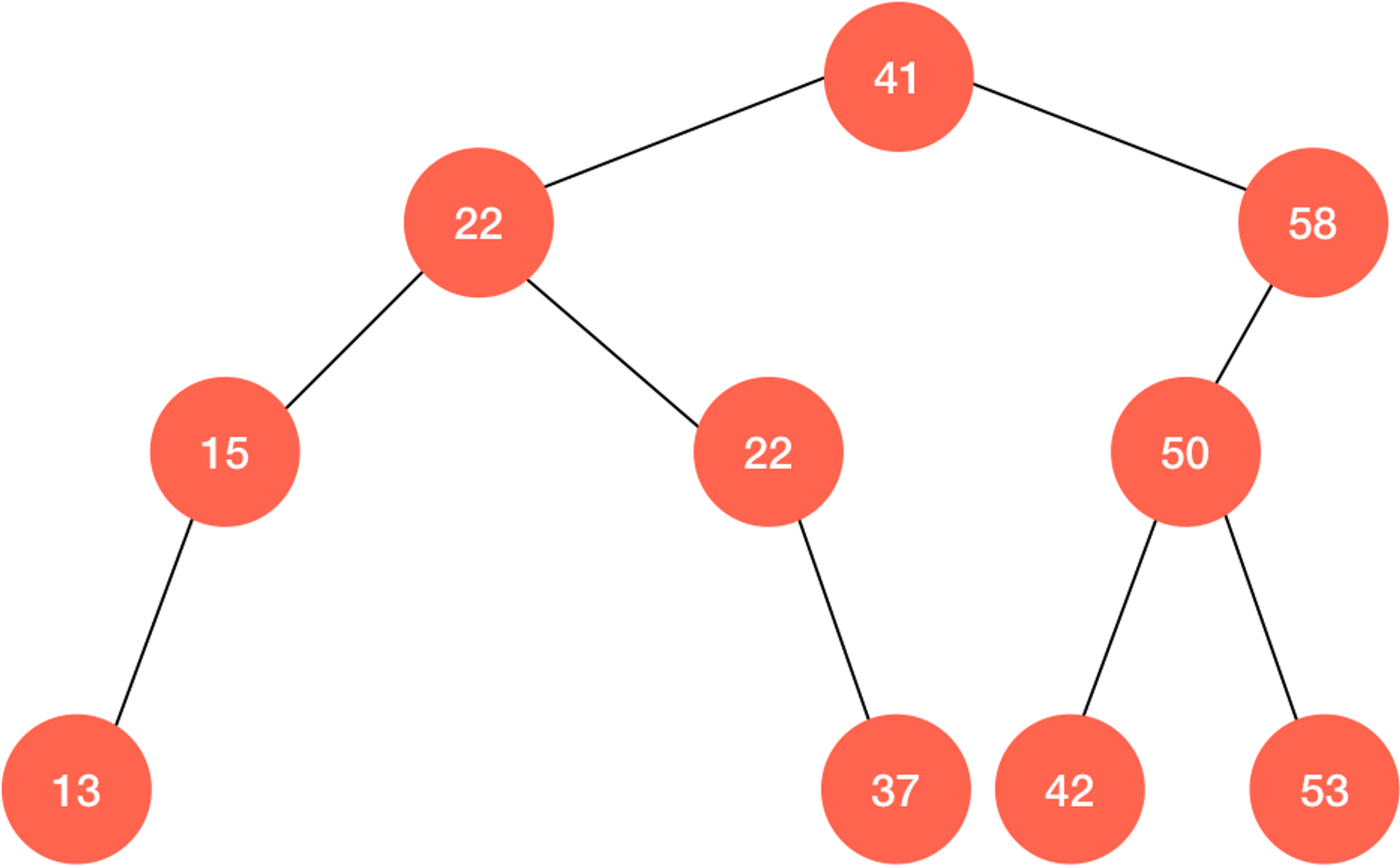
有了这些性质,我们很容易就能实现一个二分搜索树的基本框架:
// 二分搜索树中的节点的结构体
class Node {
constructor (k, v) {
this.key = k
this.value = v
this.left = null
this.right = null
}
}
// 二分搜索树
class BinarySearchTree {
constructor () {
this.root = null
this.count = 0
}
// 返回二分搜索树的节点个数
size () { return this.count }
// 返回二分搜索树是否为空
isEmpty () { return this.count === 0 }
// 向二分搜索树中插入一个新的(k, v)数据对
insert (k, v) {
// TODO: 稍后实现
}
contain (k) {
// TODO: 稍后实现
}
search (k) {
// TODO: 稍后实现
}
}插入元素
简单来说,记带插入元素
s 为 (k, v),插入元素的算法流程可以表述为:- 若带插入的树根节点
node为空,则将带插入元素作为根节点插入;否则:
- 若
k等于node.key,则更新node.value为v;否则:
- 若
k小于node.key,则将带s插入到node的左子树中;否则:
- 将
s插入到node的右子树中。
动画演示:
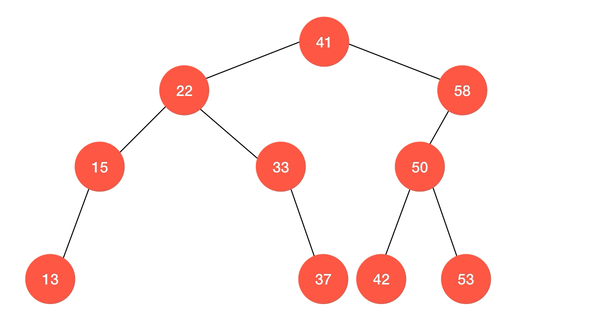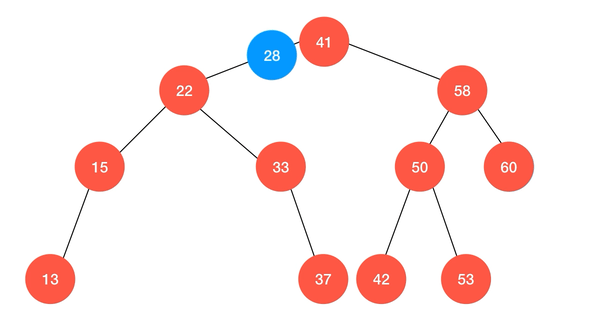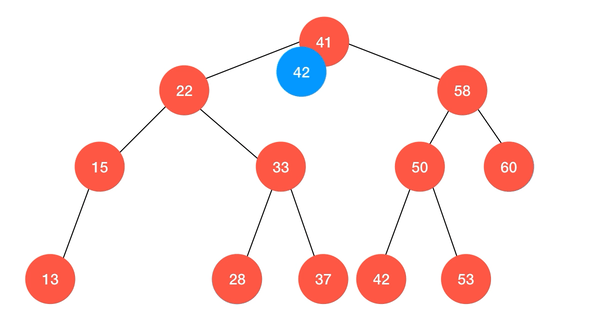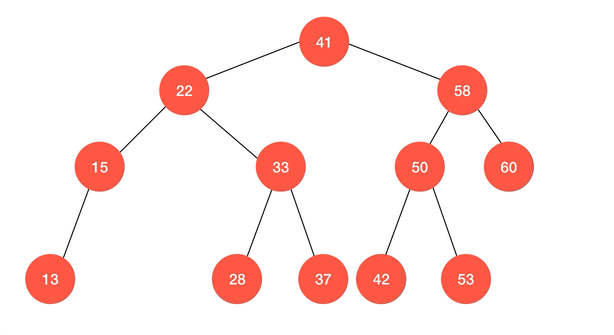
// 向以 node 为根的二分搜索树中, 插入节点 (k, v), 使用递归算法
// 返回插入新节点后的二分搜索树的根
function insert (node, k, v) {
if (node === null) {
return new Node(k, v)
}
if (k === node.key) {
node.value = v
} else if (k < node.key) {
node.left = insert(node.left, k, v)
} else {
node.right = insert(node.right, k, v)
}
return node
}
class BinarySearchTree {
...
insert (k, v) {
this.root = insert(this.root, k, v)
this.count += 1
}
...
}查找元素
简单来说,在以
node 为根节点的二分搜索树中查找一个元素 v 的算法过程可以简述为:- 若
node为空则查找失败;否则:
- 若
v等于node.value则查找成功;否则:
- 若
v小于node.value,则搜索左子树;否则:
- 重复
1-4,搜索右子树。
最基本的,
contain 操作只会判断一个要查找的键是否在二分搜索树中:function contain (node, k) {
if (node === null) {
return false
}
if (k === node.key) {
return true
} else if (k < node.key) {
return contain(node.left, k)
} else {
return contain(node.right, k)
}
}
class BinarySearchTree {
...
contain (k) { return contain(this.root, k) }
...
}略微复杂一点的,
search 操作则要找到带查找的对应节点:function search (node, k) {
if (node === null) {
return null
}
if (k === node.key) {
return node.value
} else if (k < node.key) {
return search(node.left, k)
} else {
return search(node.right, k)
}
}
class BinarySearchTree {
...
search (k) { return search(this.root, k) }
...
}不难看出,
search 操作分返回形式其实有很多种,我在这里只是简单的将存储的值返回给用户,要知道,在 JavaScript 语言中,只有 Object、Function、RegExp 等类型的对象是通过引用传参的,其他的像 Number、Boolean、String 等基本类型都是通过拷贝值传参,那么就要注意如果你直接在 value 中存放基本类型,你在外部将无法修改树内存储的数据,这显然是不可接受的。当然,你可以将找的节点直接返回给用户,但我非常不推荐这样做,这样一来你就会将树内部的数据结构暴露给用户,用户往往不需要甚至不理解如何维护内部数据结构,这样导致的问题就是用户有意或无意中修改了诸如
key 甚至 left、right 一类的成员,将直接导致数据结构崩坏,进而使程序崩溃。小结
在这一小节中我们学习了二分查找法这种基本的搜索算法,也了解并实现了一个基本的二分搜索树的类型,并实现了插入和查找两个基本的操作,在下一小节中我们将学习到二分搜索树的重点,也是它非常重要的几个操作:遍历操作。