【慕课】重学算法 - part.4 二分搜索树 (2)

这系列文章是慕课网《算法与数据结构》实战课程老师的讲授内容笔记整理，其中有很多动图都是我参考老师的动画演示自己制作的，并提供 JS(es6) 版的代码示例。代码仓库：📦 https://github.com/Mitscherlich/Play-with-Algorithms-JS

上一小节中我们实现了二分搜索树的插入和查找连个基本操作，在本小节中我将为大家介绍二分搜索树的遍历操作。遍历是也一个非常普遍的算法，在本系列的后续中我们还将学到图相关的数据结构，届时也要学习图相关的遍历操作。

在开始之前，我们首先需要补充一下上一节实现的二分搜索树的定义：

class BinarySearchTree {
  ...
  // 前序遍历
  preOrderTraverse (cb) {
    // TODO: 稍后实现
  }
  // 中序遍历
  inOrderTraverse (cb) {
    // TODO: 稍后实现
  }
  // 后序遍历
  postOrderTravse (cb) {
    // TODO: 稍后实现
  }
  // 层序遍历
  levelOrderTravse (cb) {
    // TODO: 稍后实现
  }
  ...
}

稍后我们就要来实现这其中的几个操作。

遍历元素

我们要遍历一棵树的所有元素，首先想到的就是本科时已经学习过的树的三种遍历算法：前序遍历、中序遍历和后序遍历。无论是那种遍历算法，我们都可以抽象的将一棵将要遍历的树分成三部分：要访问的节点本身、它的左子树以及它的右子树：

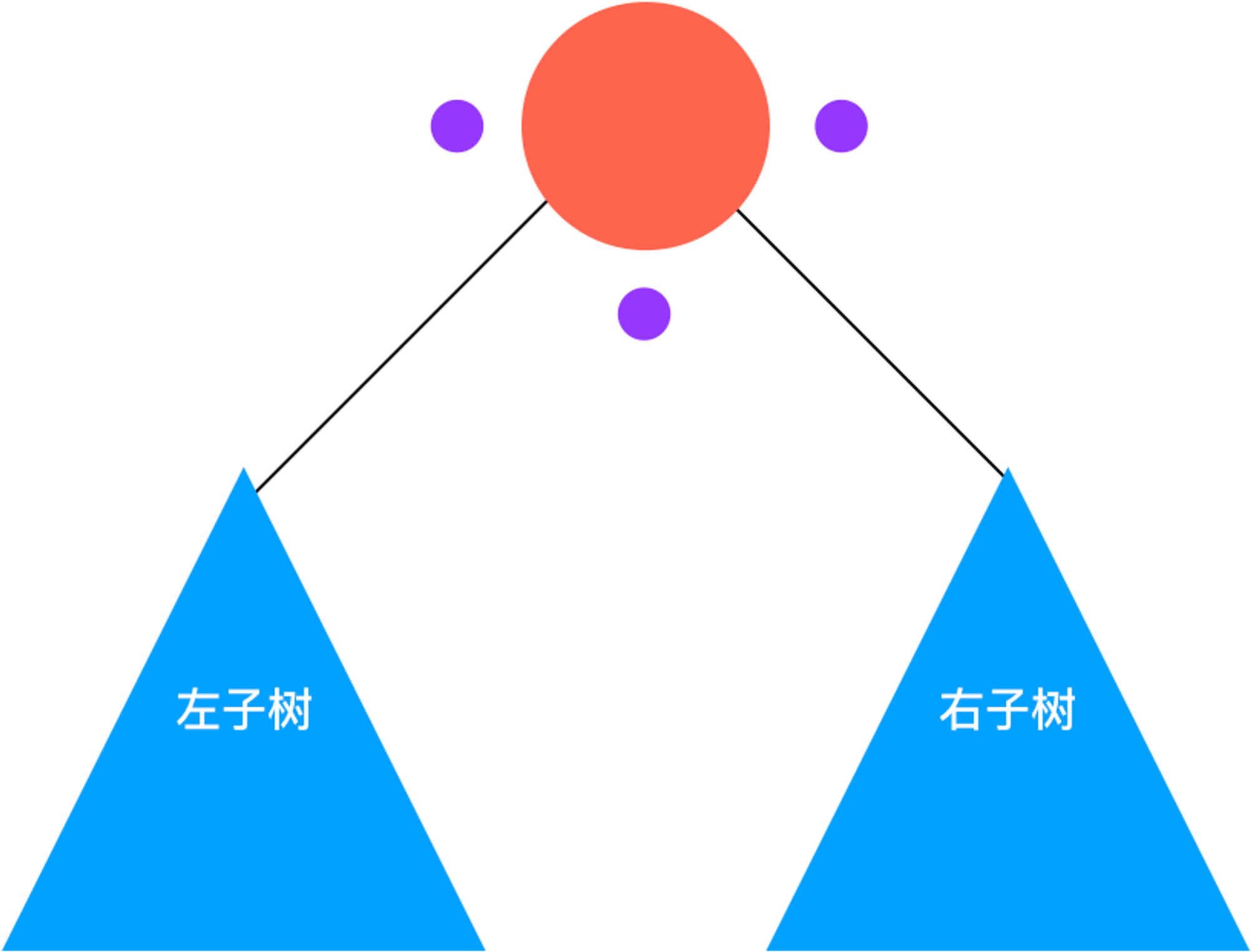
前(中/后)序遍历的差别只在于什么时候对要访问的节点进行具体操作；而对于二分搜索树这种具有特殊定义的二叉树而言，这三种遍历方式又有了新的实际意义，下面我们就分别来实现一下。

前序遍历

前序遍历顾名思义，就是先对要访问的节点进行一系列操作，然后再递归的访问它的左子树和右子树；简单来说，前序遍历以 node 为根的二分搜索树的算法流程可以表述为：

访问 node 本身；

递归访问 node 的左子树 node.left；

递归访问 node 的右子树 node.right。

动画演示：

/**
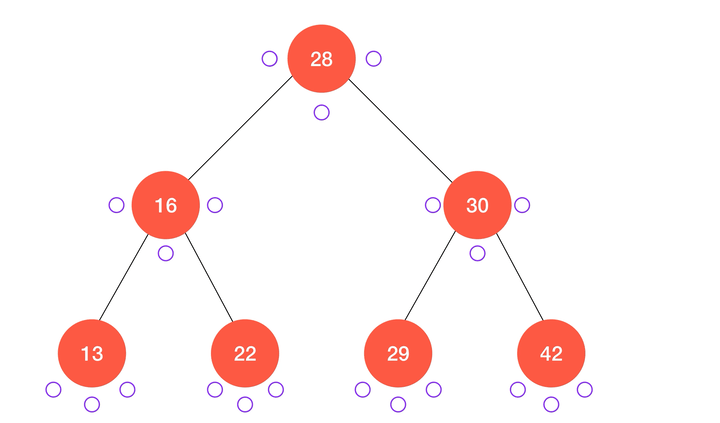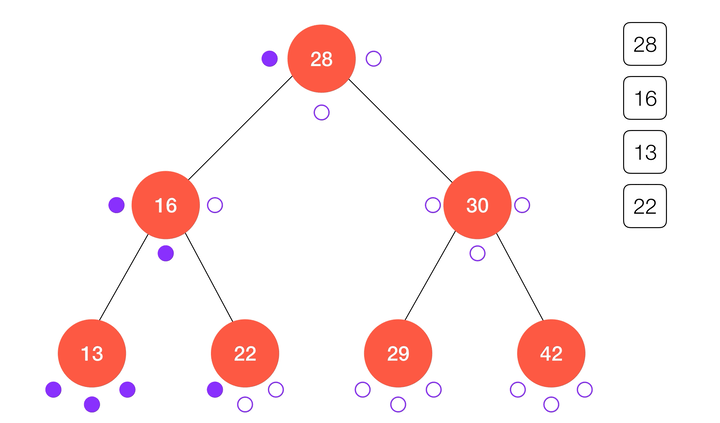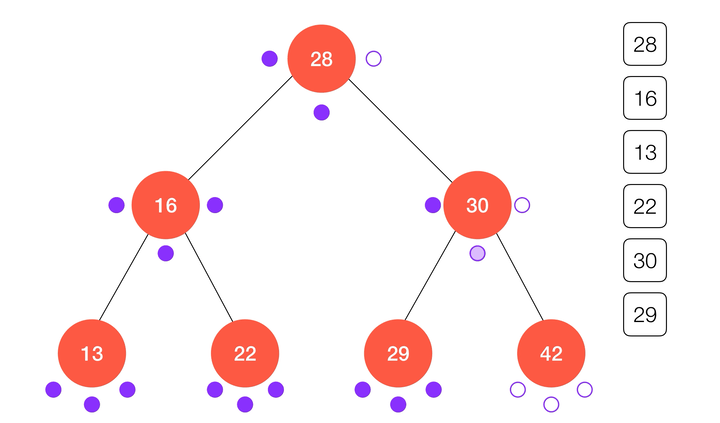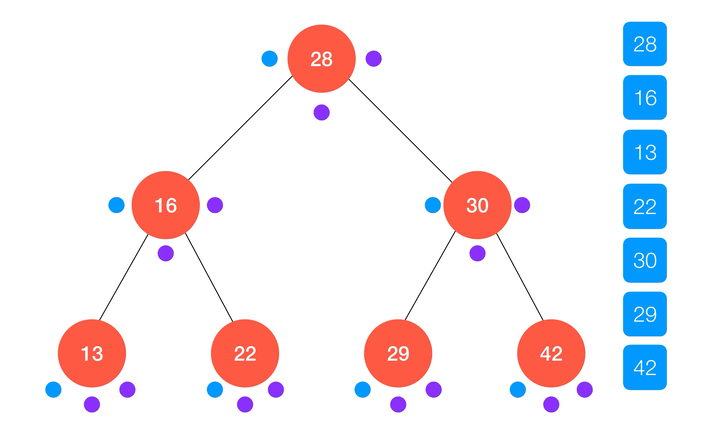
 * 对以 node 为根的二叉搜索树进行前序遍历
 * @param {Node} node 待遍历的二叉树的根
 * @param {Function} cb 遍历时的回调函数
 */
function preOrderTravse (node, cb) {
  if (node !== null) {
    cb(node)
    preOrderTravse(node.left, cb)
    preOrderTravse(node.right, cb)
  }
}

class BinarySearchTree {
  ...
  // 前序遍历
  preOrderTraverse (cb) {
    preOrderTraverse(this.root, cb)
  }
  ...
}

示例代码 src/05-Binary-Search-Tree/05-Binary-Search-Tree-Traverse.js

中序遍历

中序遍历与前序遍历类似，只不过访问顺序有所不同；简单来说，中序遍历以 node 为根的二分搜索树的算法流程可以表述为：

递归访问 node 的左子树 node.left；

访问 node 本身；

递归访问 node 的右子树 node.right。

动画演示：

💡

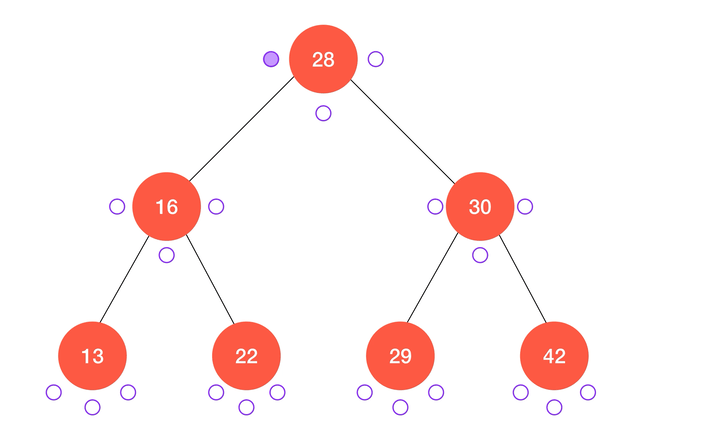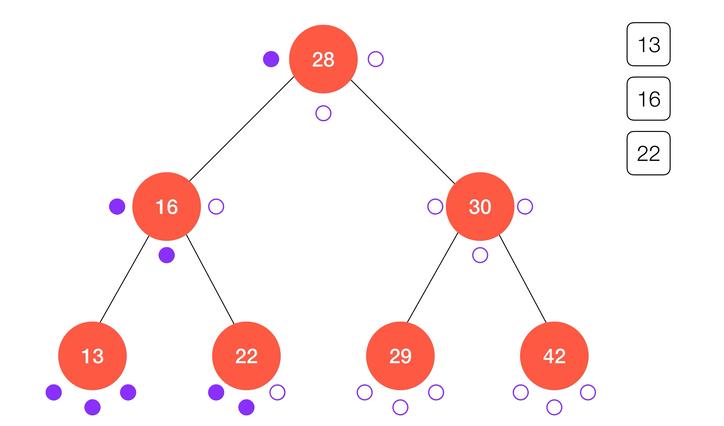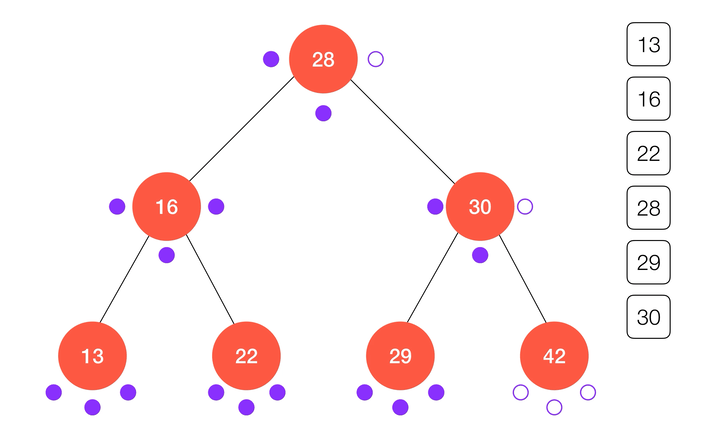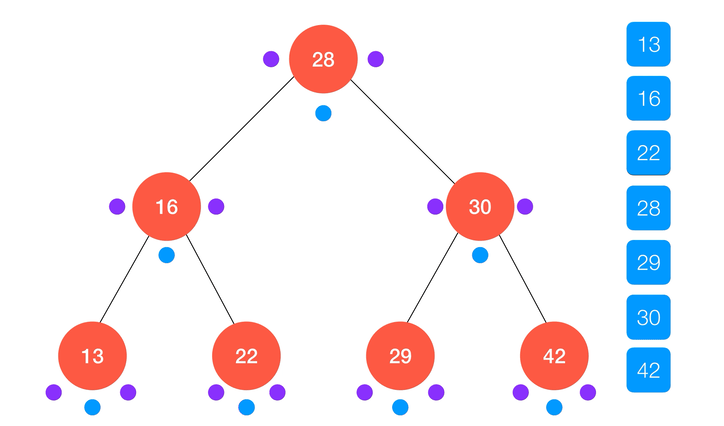
不难看出，中序遍历的结果正好使得键值从小到大进行了排序，这也是得益于二分搜索树的定义，同时也是二分搜索树的应用之一

/**
 * 对以 node 为根的二叉搜索树进行中序遍历
 * @param {Node} node 待遍历的二叉树的根
 * @param {Function} cb 遍历时的回调函数
 */
function inOrderTravse (node, cb) {
  if (node !== null) {
    inOrderTravse(node.left, cb)
    cb(node)
    inOrderTravse(node.right, cb)
  }
}

class BinarySearchTree {
  ...
  // 中序遍历
  inOrderTraverse (cb) {
    inOrderTraverse(this.root, cb)
  }
  ...
}

后序遍历

类似的，后序遍历的算法流程可以表述为：

递归访问 node 的左子树 node.left；

递归访问 node 的右子树 node.right；

访问 node 本身。

动画演示：

/**
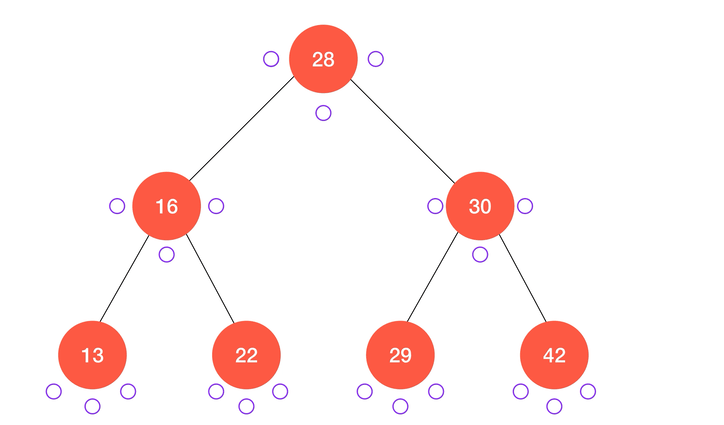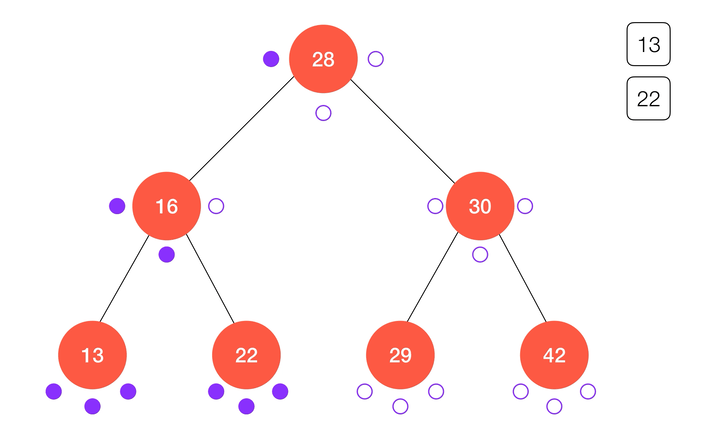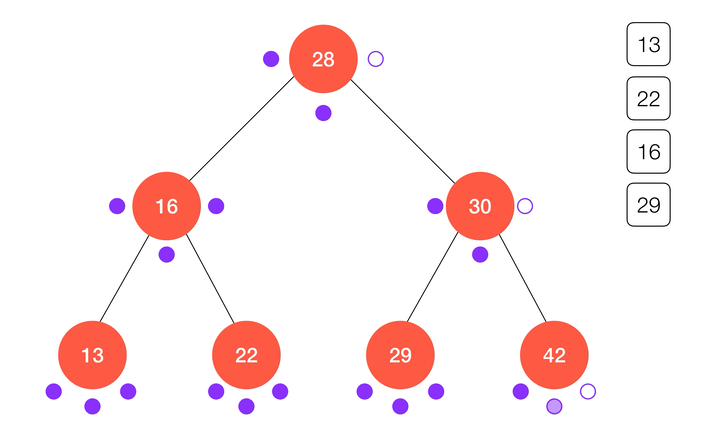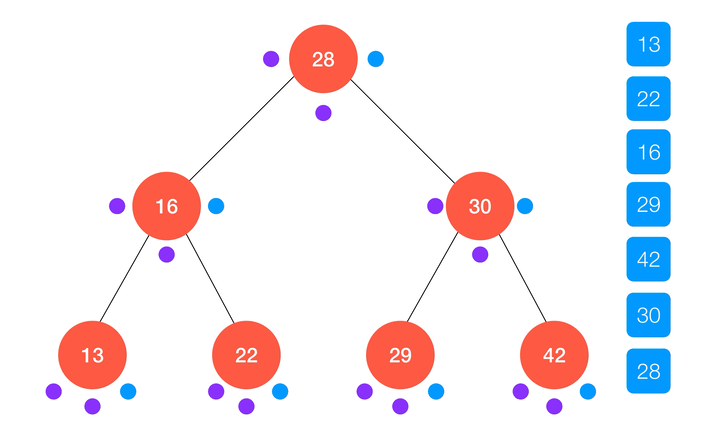
 * 对以 node 为根的二叉搜索树进行后序遍历
 * @param {Node} node 待遍历的二叉树的根
 * @param {Function} cb 遍历时的回调函数
 */
function postOrderTravse (node, cb) {
  if (node !== null) {
    postOrderTravse(node.left, cb)
    postOrderTravse(node.right, cb)
    cb(node)
  }
}

class BinarySearchTree {
  ...
  // 后序遍历
  postOrderTravse (cb) {
    postOrderTravse(this.root, cb)
  }
  ...
}

后序遍历同样也有它的用途。虽然在 JavaScript 语言中我们不要进行垃圾回收，但类似 C/C++ 这样的语言或许需要用户自己管理内存。例如在析构一棵二分搜索树时，我们要保证每个节点分配的空间都被释放了，就需要用到后序遍历的方法；正如演示的那样，后序遍历总是在处理完左右子树之后再回来处理节点本身，这样就保证了析构的顺序性。

层序遍历

二叉树还有一类特殊的遍历方法，称为层序遍历。顾名思义，这种方式将一层一层的逐层访问二叉树，从深度为 1 的根节点一直到叶子结点。这是我们就需要借助其他的数据结构来完成层序遍历的操作了。最经典的实现是借助一个队列；简单来说，层序遍历一棵以 node 为根的二分搜索树，其算法流程可以表述为：

node 入队，遍历队列，若队列为空则结束遍历；否则：

访问队首元素，将队首元素的左右孩子入队；

重复 1-2 知道 1 中的条件不满足或遍历完成。

动画演示：

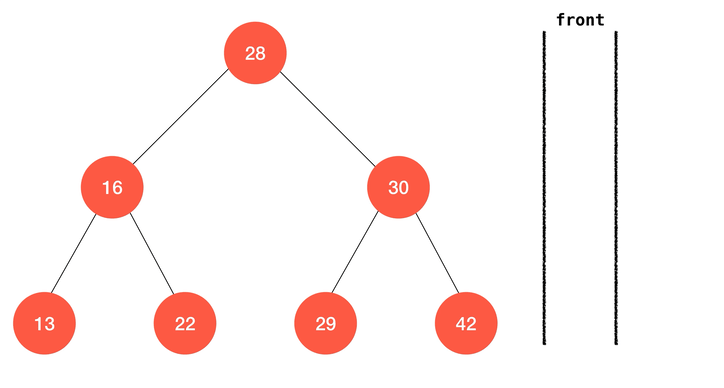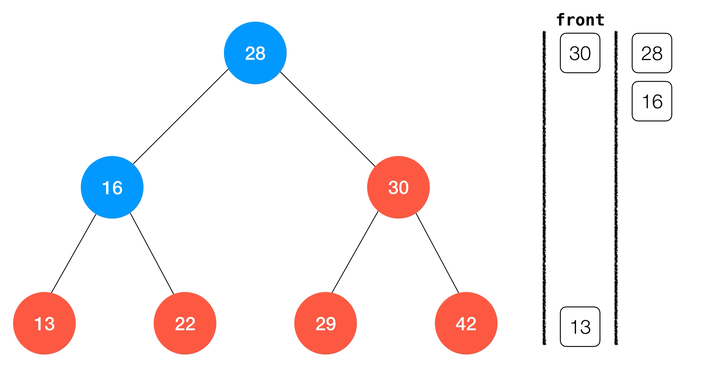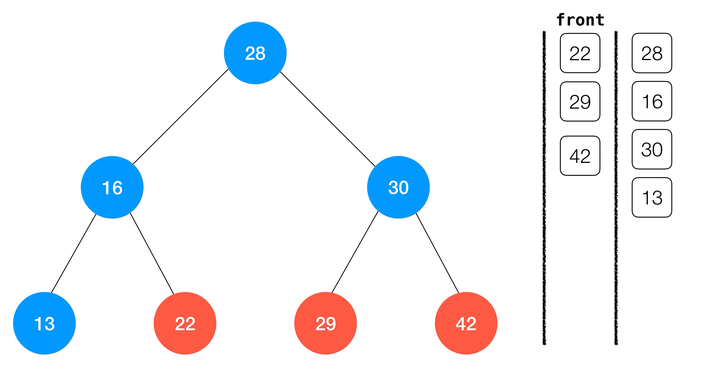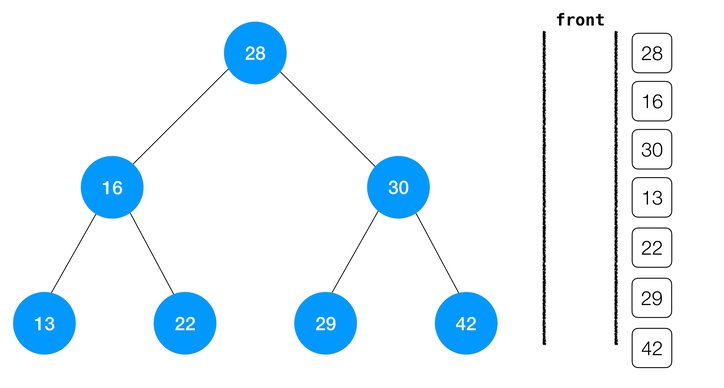
class BinarySearchTree {
  ...
  // 层序遍历
  levelOrderTravse (cb) {
    // 根节点入队
    const queue = [ this.root ]
    // 队列非空
    while (queue.length > 0) {
      // 队首出队
      const node = queue.shift()
      // 访问队首节点
      cb(node)
      // 若左孩子非空
      if (node.left !== null) {
        // 左孩子入队
        queue.push(node.left)
      }
      // 若右孩子非空
      if (node.right !== null) {
        // 右孩子入队
        queue.push(node.right)
      }
    }
  ...
}

小结

广义来讲，上面我们介绍的遍历算法其实分为两大类：深度优先遍历 (DFS)和广度优先遍历 (BFS)；其中前/中/后序遍历就属于深度优先遍历，这种遍历方法顾名思义，就是不断递归直到访问到最深一层的节点；相对地，层序遍历就属于广度优先遍历，相比较深度优先遍历，广度优先需要尝试性的访问一个节点的所有邻接点，然后在从一个邻接点的后继继续访问。

这两种遍历算法算法各有不同的应用，例如 DFS 就常被用于解决各类迷宫；而 BFS 则常被用于各类搜索引擎的数据爬虫中。在后续图的相关算法中，我们还将看到这两个算法熟悉的身影。在下一节中我们将实现二分搜索树最复杂的一类操作：删除操作。

参考链接

二叉搜索树 - 维基百科