这系列文章是慕课网《算法与数据结构》实战课程老师的讲授内容笔记整理,其中有很多动图都是我参考老师的动画演示自己制作的,并提供 JS(es6) 版的代码示例。代码仓库:📦 https://github.com/Mitscherlich/Play-with-Algorithms-JS
这里所指的堆并不是本科学习中常见到的堆栈的一部分。事实上,堆作为一个独立的数据结构,它的实现形式通常是一棵树;而堆栈(简称栈)是一种线性的数据结构。本小节就来为大家介绍堆这种数据结构,并实现堆的一个特殊形式 —— 最大堆,并由此引出一种常用的排序算法:堆排序。

堆与优先队列
在介绍堆这种数据结构之前,我更想先介绍一下它在解决实际问题中的一个典型应用:优先队列。我们已经学习过队列这种数据结构,对于队列而言,有两个最核心的操作:出队和入队。
这两个操作只会发生在队首和队尾,但在实际应用中我们通常需要处理这样一类问题:从队列中选择一个特定的元素让它出列,一个典型的例子是操作系统在处理一系列作业时,需要根据一定的优先级按序执行这些作业,优先级高的任务先被调度;这样就要求队列形成一种被称为优先队列的数据结构,也就是具有优先权的队列。而堆这个数据结构正是被设计用来解决这一类问题。
堆的定义和实现
要使用堆实现优先队列的操作,我们首先要实现堆的数据结构。我们采用最经典的实现形式:二叉堆。
二叉堆以及它的性质
相应的,二叉堆的实现形式很像一棵二叉树(即每个节点最多只有两个子节点)。要使得这样的二叉树成为堆,还应该满足以下性质:
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,而最底层则尽可能地从左到右填入;
- 堆序性:任意节点小于(或大于)它的所有子节点,且根节点为最小或最大的元素。
根据堆序性,又将根节点为最大元素的堆称为最大堆,根节点为最小元素的堆称为最小堆。
最大堆和最小堆的实现相当类似,本小节则以最大堆为例进行讲解。
最大堆的实现
我们在本科学习中很可能都实现过树,或者具体来说,二叉树这种数据结构。那么大家都很可能想到继续用树这种数据结构来存放堆。而这里为大家介绍一种很经典的方法:用数组存放二叉堆。
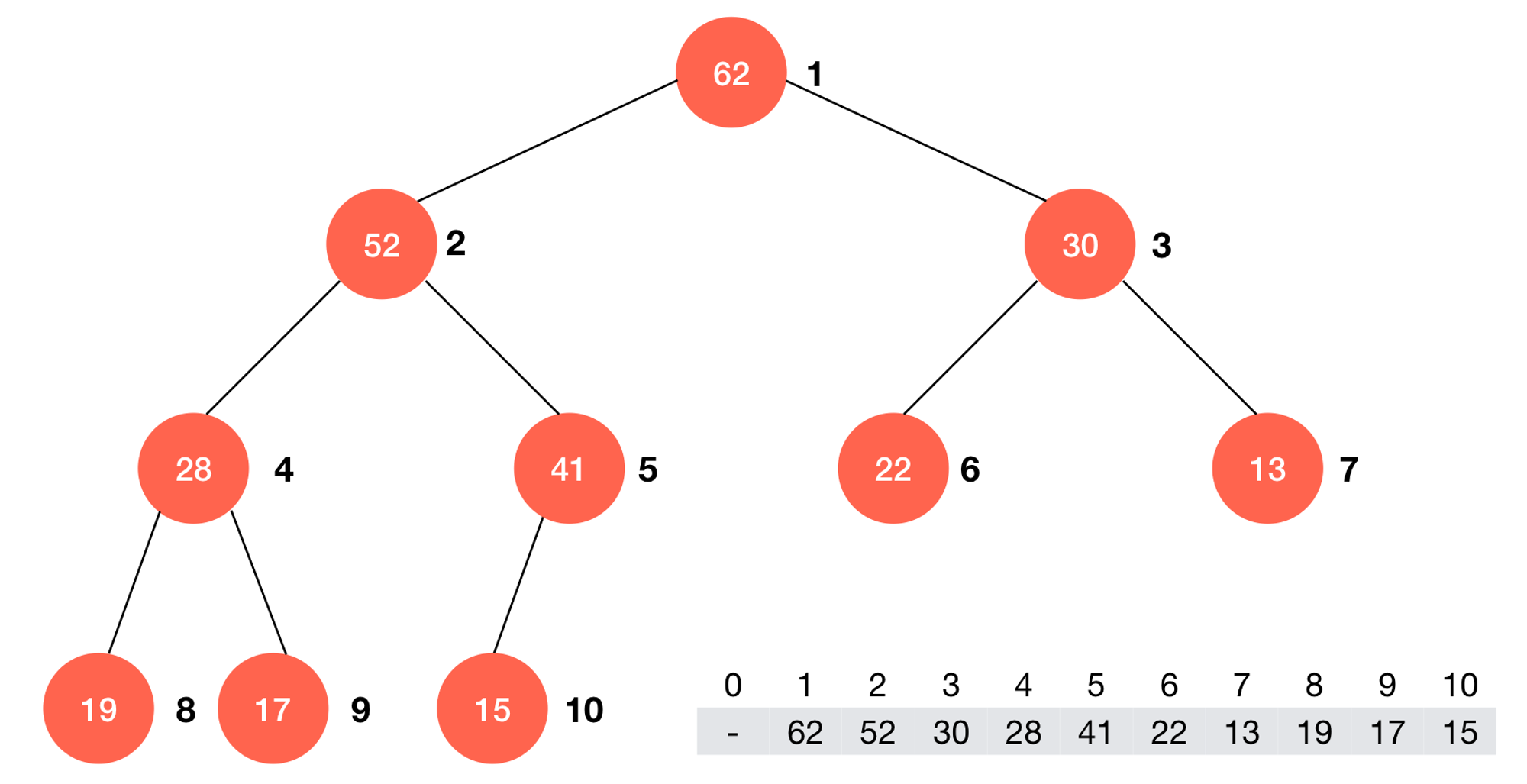
我们之所以可以使用数组来存放二叉堆,正是因为二叉堆有一个重要的性质:总是一棵完全二叉树。如图,我们将二叉堆从上到下、从左到右的标上序号,则可以发现:二叉堆的每一个元素都可以与数组的某个下标相对应。
如果用
i 来表示某个对应的节点,则很容易发现:它的左孩子节点编号为 2i,右孩子节点编号为 2i+1。但注意,这条规律只适用于如图方式标记的二叉堆,因为在这里我将根结点记为了 1,而如果你将根结点从 0 开始编号,也很容易得到类似的性质,这用数学归纳法很容易证明。下面的代码提供了最基本的最大堆
MaxHeap 类的定义:// 使用了 es6 的 class 语法糖,和 es5 的功能是一样的
class MaxHeap {
// 构造函数, 构造一个空堆, 可容纳 capacity 个元素
constructor (capacity) {
this.#capacity = capacity
this.#count = 0 // es9 草案的私有成员声明方法
// 无法直接使用 (babel 也不行)
// 请不要直接复制粘贴 :)
this.#data = new Array(capacity + 1)
}
// 获取元素个数
size () {
return this.#count
}
// 判断是否为空
isEmpty () {
return this.#count === 0
}
// 与 string 类型的转换
toString () {
return JSON.stringify(this.#data)
}
// 插入元素
insert (item) {
// TODO: 稍后实现
}
// 出堆元素: 总是最大的元素出堆
extractMax () {
// TODO: 稍后实现
}
}暂时还没有实现的方法有入队操作
insert 和出队操作 extractMax,接下来我们要一一实现它们。- 插入元素 (Shift Up)
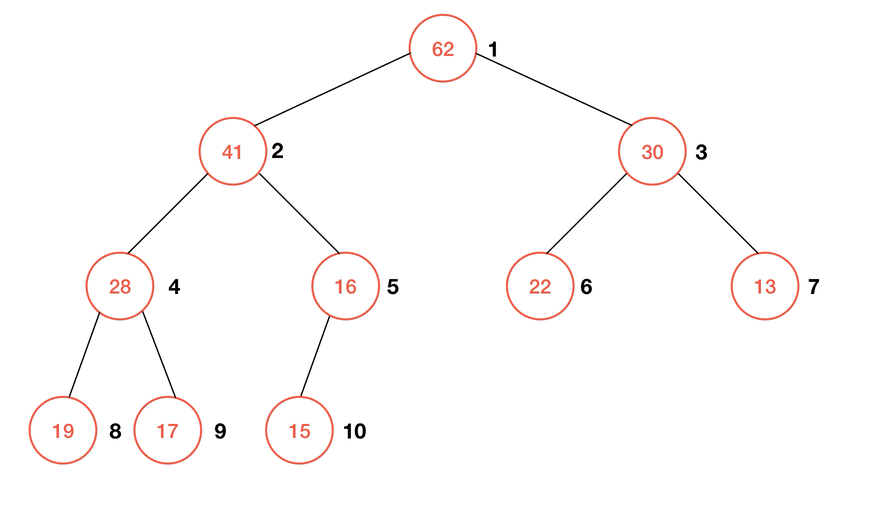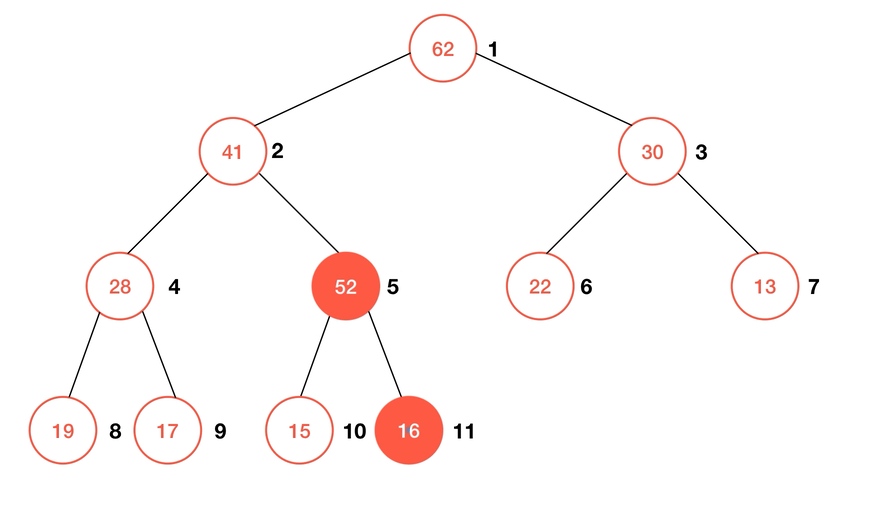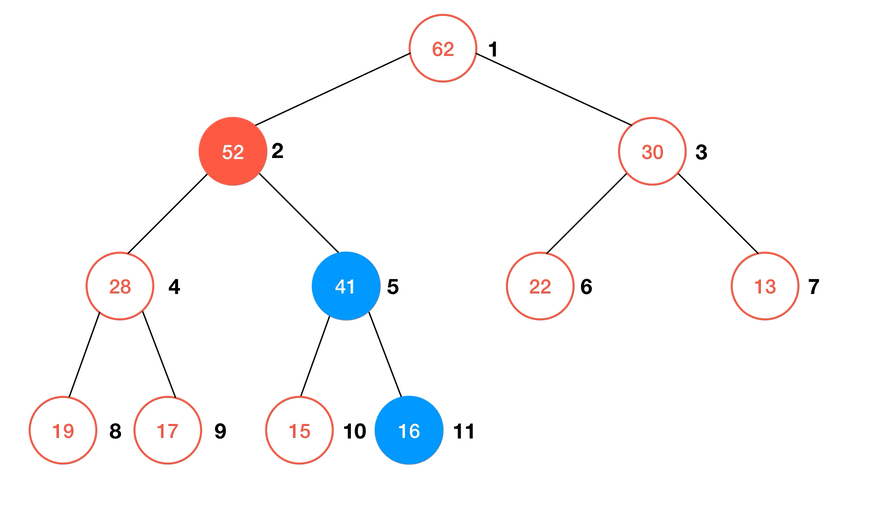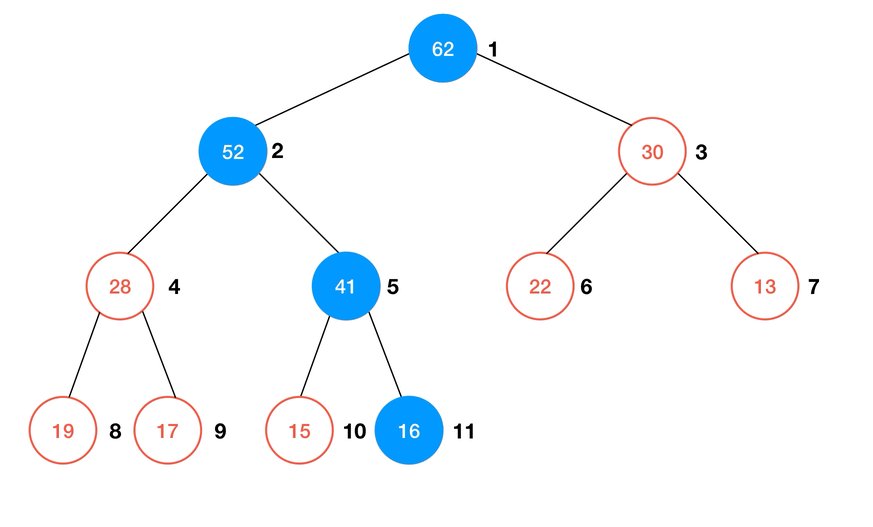
要实现在堆中插入一个元素的操作,我们要通过一个被称为 Shift Up 的子过程。由于使用数组来存储堆,这使得我们只需要在数组的末尾加上一个新的元素,再通过
shiftUp 来使得数组重新形成一个最大堆就可以了。简单来说,shiftUp 的算法可以描述为:- 若待
shiftUp的元素不是根结点,则与其父节点比较,若: a. 若大于父节点,则与之交换位置; b. 否则结束比较;
- 重复直至不满足
1中的条件。
动画演示:
了解了
shiftUp 的过程,我们就可以实现堆的插入操作了:// shift up 操作
function shiftUp (data, k) {
while (k > 1 && data[Math.floor(k / 2)] < data[k]) {
// swap(data[k/2], data[k])
[data[Math.floor(k / 2)], data[k]] = [data[k], data[Math.floor(k / 2)]]
k = Math.floor(k /= 2)
}
}
class MaxHeap {
...
// 插入操作
insert (item) {
if (this.#count + 1 < this.#capacity) {
return // 在这里,我让容量不足的情况直接返回
// 事实上,JS 很容易就能实现数组的扩展
// 大家可以自行思考并实现扩容操作
}
this.#count += 1
this.#data[this.#count] = item
shiftUp(this.#data, this.#count)
}
...
}类似的,
shiftUp 也有一个显而易见的优化,就是每次比较不直接交换位置,而是找到合适的后通过一次赋值实现交换:function shiftUpEnhance (data, k) {
const e = data[k]
while (k > 1 && data[Math.floor(k / 2)] < e) {
// swap(data[k/2], data[k])
data[k] = data[Math.floor(k / 2)]
k = Math.floor(k /= 2)
}
data[k] = e
}- 删除元素 (Shift Down)
删除元素,或者说从堆中取出一个元素,则需要另一个子过程 Shift Down。在最大堆中,我们总是取出最大的元素,也就是根元素,同时也是数组
1 号索引所对应的元素。这时的堆自然也就缺少了一个元素,为了使现在的数组重新形成完全二叉树,只需要将此时数组末尾的元素赋值给根节点即可,再通过 shiftDown 来维护堆序性。简单来说,shiftDown 的过程描述为:- 若待
shiftDown的元素不是叶子结点,则与其子节点中较大的比较,若: a. 仍大于较大的节点元素,则与之交换位置; b. 否则结束比较;
- 重复直到
1中的条件不满足。
动画演示:
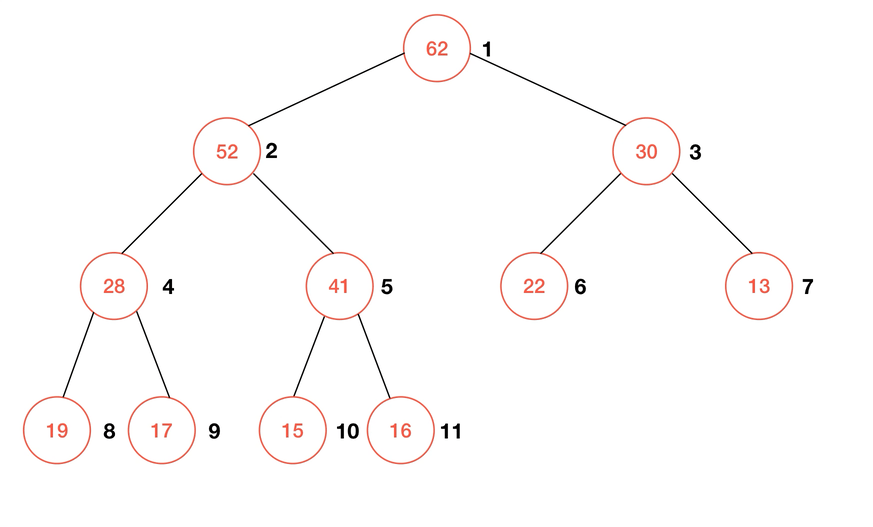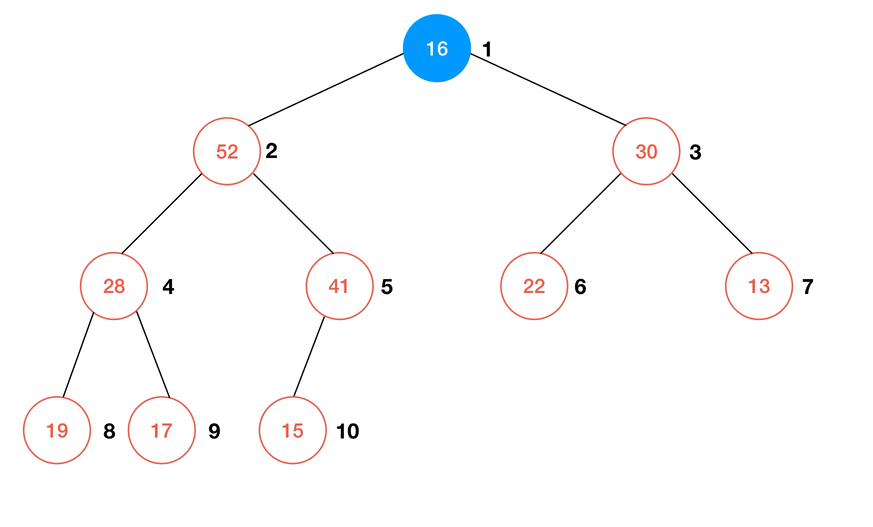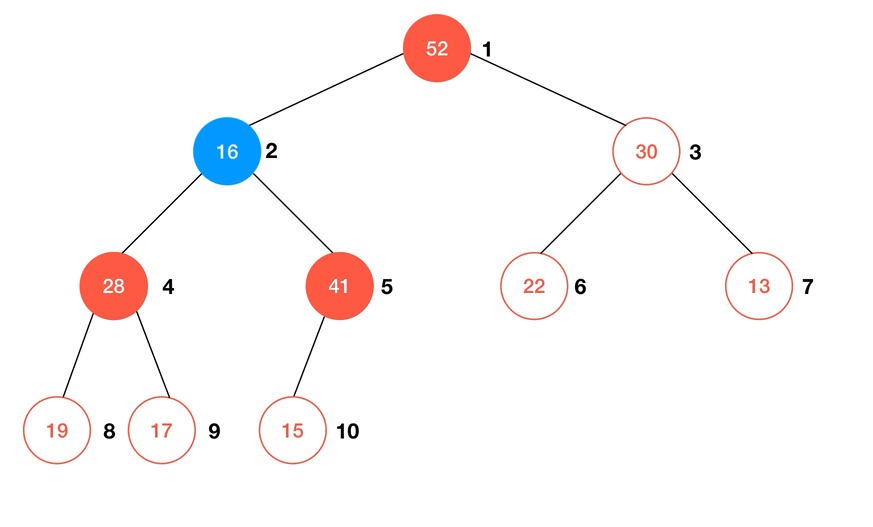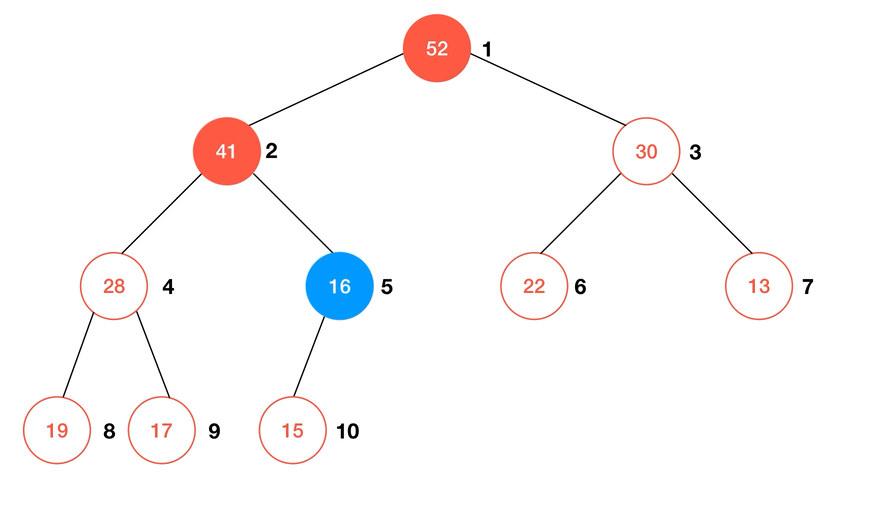
使用
shiftDown 操作,我们同样可以方便的实现取出元素的操作:// shift down 操作
function shiftDown (data, k, count) {
while (2 * k <= count) {
let j = 2 * k // 此轮循环中, swap(data[k], data[j])
if (j + 1 <= count && data[j + 1] > data[j]) {
j++
}
if (data[k] >= data[j]) {
break
}
// swap(data[k], data[j])
[data[k], data[j]] = [data[j], data[k]]
k = j
}
}
class MaxHeap {
...
// 出堆元素: 总是最大的元素出堆
extractMax () {
const ret = this.#data[1]
;[this.#data[1], this.#data[this.#count]] = [this.#data[this.#count], this.#data[1]]
this.#count -= 1
shiftDownEnhance(this.#data, 1, this.#count)
return ret
}
...
}类似的,一步交换优化
shiftDown 操作:function shiftDownEnhance (data, k, count) {
const e = data[k]
while (2 * k <= count) {
let j = 2 * k // 此轮循环中, swap(data[k], data[j])
if (j + 1 <= count && data[j + 1] > data[j]) {
j++
}
if (e >= data[j]) {
break
}
// swap(data[k], data[j])
data[k] = data[j]
k = j
}
data[k] = e
}小结
在本小节中,我为大家介绍了堆的性质及应用,并且带领大家一起实现一个基本的最大堆的类。堆的构建过程可以给我们带来很多启发,在下一节中我们就要学习更多利用堆的性质来完成的操作,并对现在的堆进行一定的优化。