【慕课】重学算法 - part.2 高级排序 (2)

这系列文章是慕课网《算法与数据结构》实战课程老师的讲授内容笔记整理，其中有很多动图都是我参考老师的动画演示自己制作的，并提供 JS(es6) 版的代码示例。代码仓库：📦 https://github.com/Mitscherlich/Play-with-Algorithms-JS

上一节我们学习了归并排序。但作为一个级别的排序算法，归并排序并没有被大规模应用在实际的系统级类库中。接下来我们将学习一个极为重要的，甚至被誉为“21世纪最重要的算法”，同时也是本系列排序算法的重点 —— 快速排序。篇幅比较长，希望大家可以耐心细读。

快速排序

Merge Sort 和 Quick Sort 都使用了分治算法

💡

分治算法: 顾名思义，分而治之。即将原问题分割成同等结构的子问题，之后将子问题逐一解决后，原问题也就得到了解决。

快速排序(简称快排)顾名思义，它很快；虽然平均时间复杂度仍然是，但通常明显比其他算法更快。我们知道归并排序是不论数组怎么样，都一刀切的将其一分为二，然后通过归并操作逐级递归的将数组排序；而快速排序之所以快，则是引入了一个被称为“划分 (Partition)”的子过程，将数组拆分成具有一定性质的两部分，使得快速排序的内层循环可以相当高效的完成。

快速排序的过程比较复杂，这里引用了维基百科的动画演示：

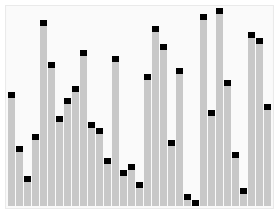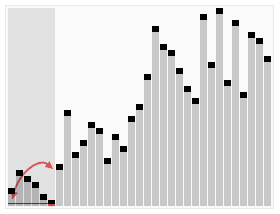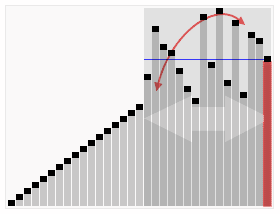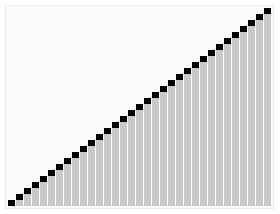
简单来说，快速排序的算法流程可以表述为：

从当前数组种选择一个元素，称为“基准 (Pivot)”

在未排序部分中为基准元素寻找合适的插入位置，并与该元素交换位置；

此时数组被分为三部分：”≤ 基准“，“基准”和“≥ 基准”，在 ”≤ 基准“和 “≥ 基准”的部分上重复 1-2，直至数组有序。

划分

不难看出，快速排序最核心的步骤就是其中的第 2 步 (划分)，也就输如何将“基准”元素放到它合适的位置，从而将原数组一分为三的。简单来说，通常我们选择待排序数组的第一个元素作为基准 v，要将数组划分为 array[l+1...j] < v 和 array[j+1...i) > v，那么划分的算法流程可以表述为：

遍历数组，与基准元素比较，如果 i 所指的元素： a. 小于基准元素，则与 j+1 所指的元素交换位置； b. 不小于则继续；

将基准元素 v 于 j 所指的元素交换位置。

比较抽象，我们还是来看一下动画演示：

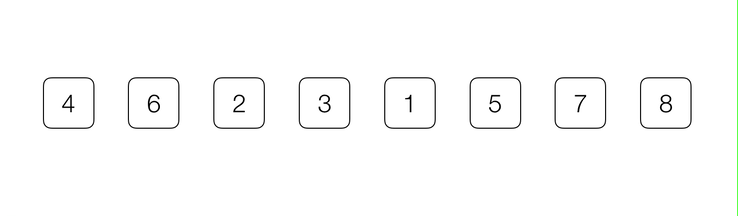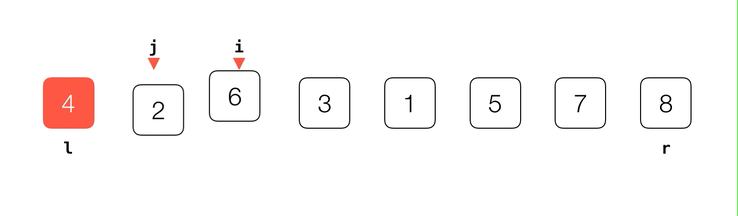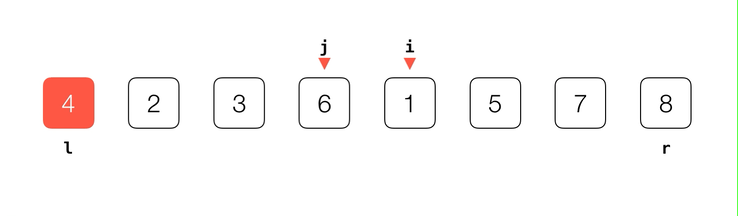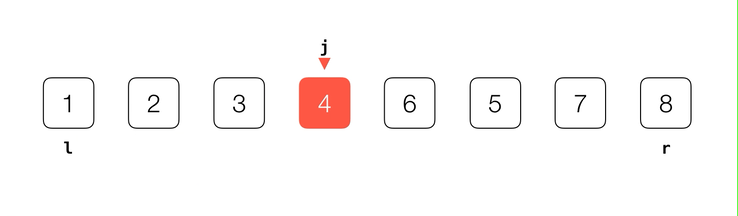
不难看出，通过不断维护 i 和 j 这两个下标，我们顺利将数组分为了 v, [l+1...j] < v 和 [j+1...i) > v 这三部分。数组遍历完成后，j 下标所指的位置就是基准元素 v 在排好序的数组中应该所处的位置。

// 对 arr[l...r] 部分进行 partition 操作
// 返回 p, 使得 arr[l...p-1] < arr[p]; arr[p+1...r] > arr[p]
function partition (array, l, r, cb) {
  const v = array[l]
  let j = l// arr[l+1...j] < v ; arr[j+1...i) > v
  for (let i = l + 1; i <= r; i++) {
    if (cb(array[i], v)) {
      j++
      [array[j], array[i]] = [array[i], array[j]]
    }
  }
  [array[l], array[j]] = [array[j], array[l]]
  return j
}

// 对 arr[l...r] 部分进行快速排序function qucikSort (array, l, r, cb) {
  if (l >= r) {
    return
  }
  const p = partition(array, l, r, cb)
  qucikSort(array, l, p - 1, cb)
  qucikSort(array, p + 1, r, cb)
}

Array.prototype.quickSort = function (cb) {
  const array = this.slice()
  const n = array.length
  qucikSort(array, 0, n - 1, cb)
  return array
}

示例代码 src/03-Sorting-Advance/05-Quick-Sort.js

类似的，我们可以用部分插入排序来优化最后的小数组排序：

// 对 arr[l...r] 部分进行快速排序
function quickSortEnhance (array, l, r, cb) {
  if (r - l <= 15) {
    insertSortPartial(array, l, r, cb)// 见【慕课】重学算法 - part.2 高级排序 (1)
    return
  }
  const p = partition(array, l, r, cb)
  quickSortEnhance(array, l, p - 1, cb)
  quickSortEnhance(array, p + 1, r, cb)
}

Array.prototype.quickSortEnhance = function (cb) {
  const array = this.slice()
  const n = array.length
  quickSortEnhance(array, 0, n - 1, cb)
  return array
}

使用 es6 解构赋值

语言特性并不是本系列的重点，但这里还是额外介绍一下使用 ECMAScript 2015 的解构赋值特性能实现的非常简单快速排序操作：

function quickSort (array) {
  if (arr.length < 2) return arr
  const [x, ...xs] = arr
  return [
    ...quickSort(xs.filter(y => y < x)),
    x,
    ...quickSort(xs.filter(y => y >= x))
  ]
}

虽然是只语法糖，但确实很好吃，不是吗？

两种特殊情况

在实际的测试用例(乱序数组))中，上面我们实现的快速排序算法已经基本满足实际使用的需要了；在使用部分插入排序后相较原始的实现性能又有略微的提升。而接下来要介绍的几种优化却是快速排序中非常重要的几个问题。

几乎有序的数组

我么知道归并排序是通过将待排序数组不断二分再归并进行排序的，这实际上形成了一颗深度为的递归树：

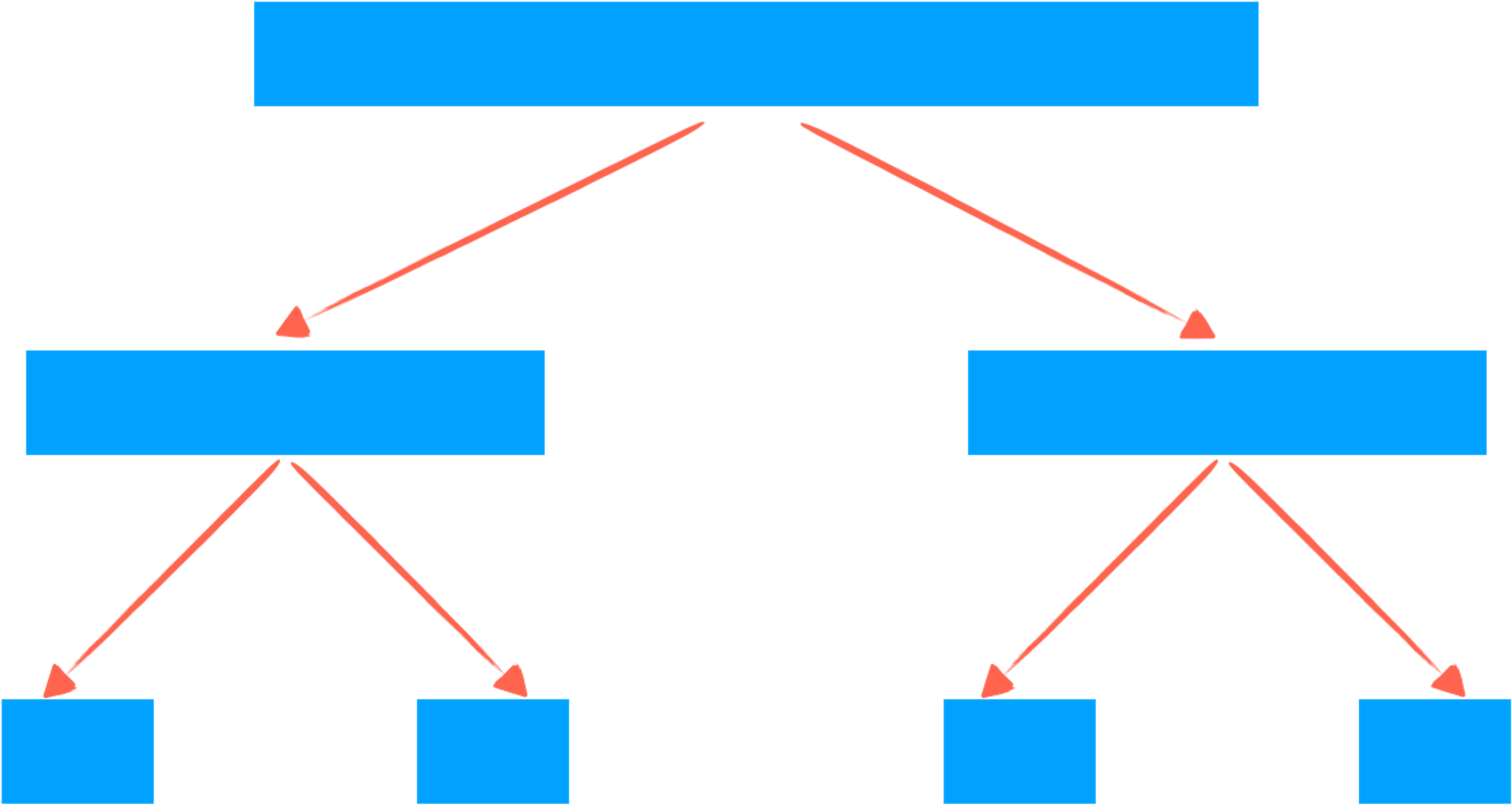
而快速排序则是通过为基准元素找合适的位置而将原数组划分，显然，大部分时候快速排序的递归树并不是平衡二叉树，而树的深度也不一定总是：

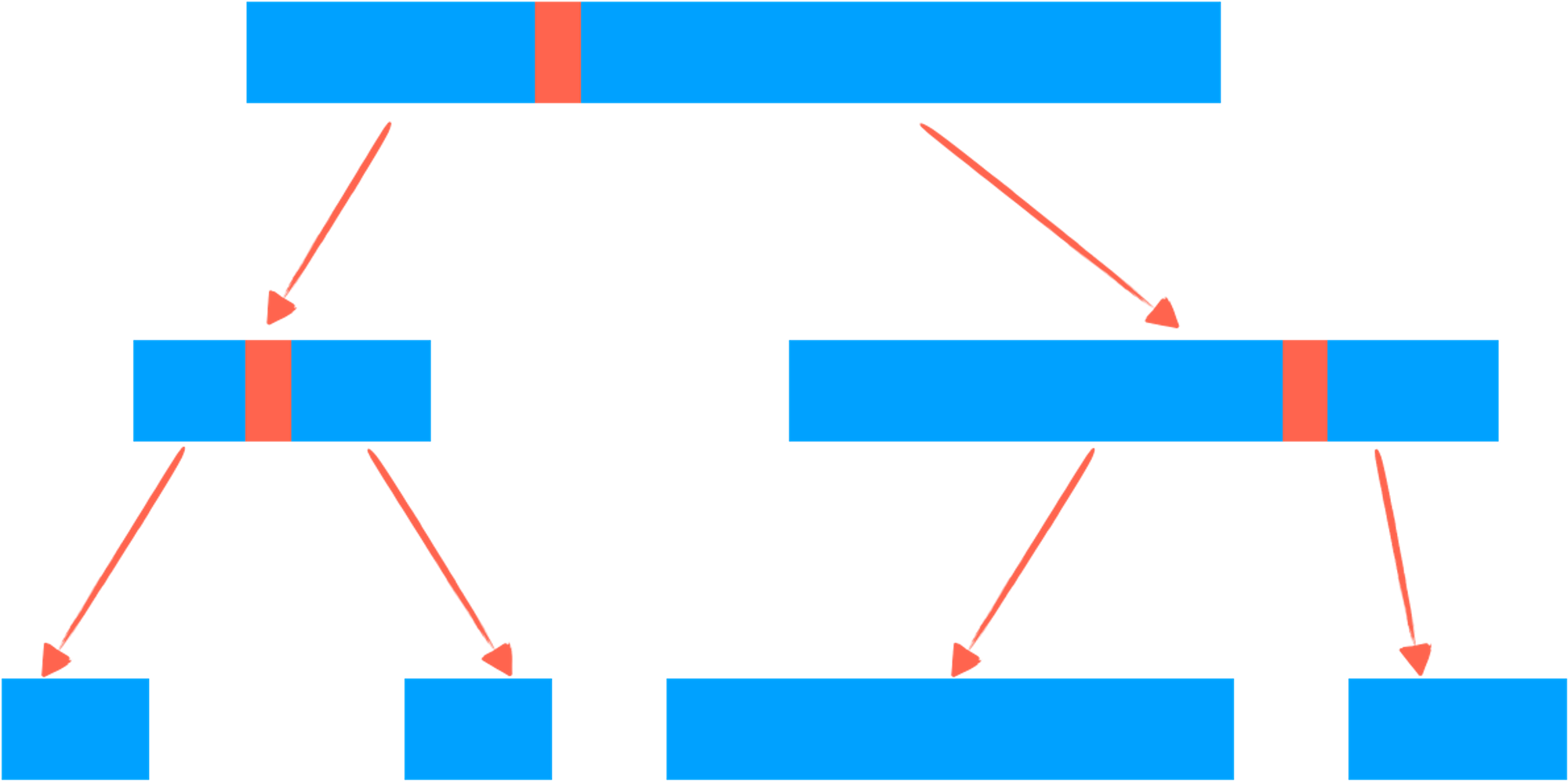
最极端的情况发生在几乎有序甚至完全有序的数组上：

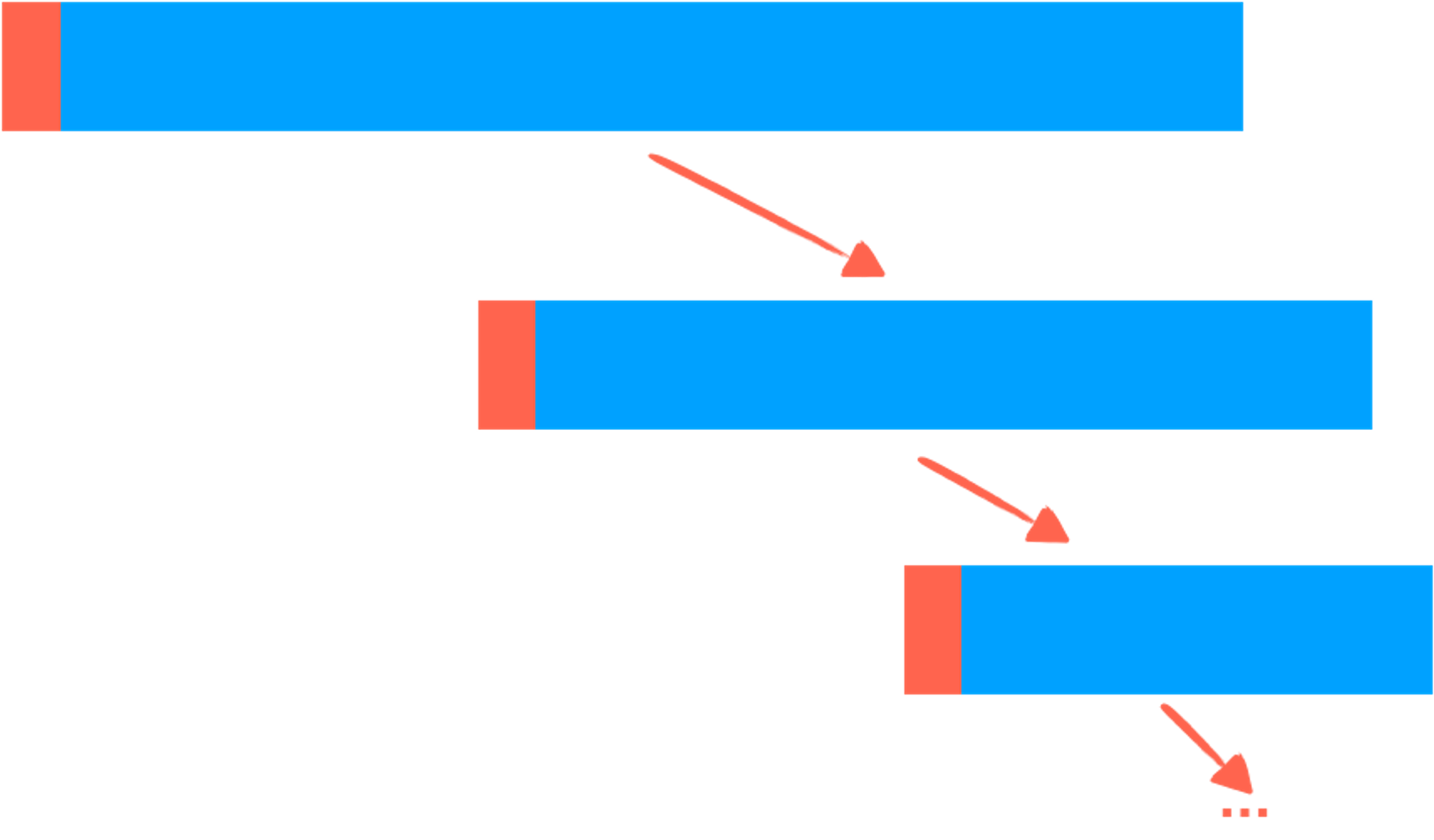
此时树的深度为，也就是说此时快速排序退化为了一个的排序算法。这显然是不可接受的。

要优化快速排序在这种情况下的问题，其实也很简单。我们现在总是选取最左的元素作为标定，但对于完全有序的数组，这就是最小(或最大)的元素，这时我们只需要用一个随机元素最为标定元素，就能使得快速排序的复杂度期望重新变成。

💡

值得注意的是，由于随机事件的存在，这种快速排序的实现并不一定总是，但数学期望总体符合。这其实很容易证明：每次随机选取到最小或最大元素的概率为，那么当元素数量足够大时，这种实现再退化为的概率将无限接近于零。

// 对 arr[l...r] 部分进行 partition 操作
// 返回 p, 使得 arr[l...p-1] < arr[p]; arr[p+1...r] > arr[p]
function partition (array, l, r, cb) {
  // 选取一个随机位置
  const k = Math.floor(Math.random() * (r - l + 1) + l)
  ;[array[l], array[k]] = [array[k], array[l]]
  const v = array[l]
  let j = l // arr[l+1...j] < v ; arr[j+1...i) > v
  for (let i = l + 1; i <= r; i++) {
    if (cb(array[i], v)) {
      j++
      [array[j], array[i]] = [array[i], array[j]]
    }
  }
  [array[l], array[j]] = [array[j], array[l]]
  return j
}

示例代码 src/03-Sorting-Advance/06-Quick-Sort-Deal-With-Nearly-Ordered-Array.js

有大量重复元素的数组

类似的，如果一个数组中的元素集中在一个很小的区间上，那么我们上面实现的快速排序算法又会退化为级别。这是由于事实上，我们并不是严格的将数组分成 < 基准和 > 基准 的两部分，而是分成了 ≤ 基准 和 ≥ 基准，这样在有大量重复元素的数组上划分出来的递归树依然极度不平衡，在最差的情况下将退化为接近级别。

了解到问题产生的原因，但这次着手改写优化相对有些不同。我们要换一种方式实现划分操作：

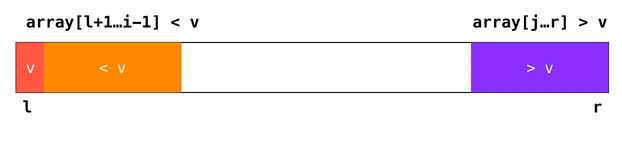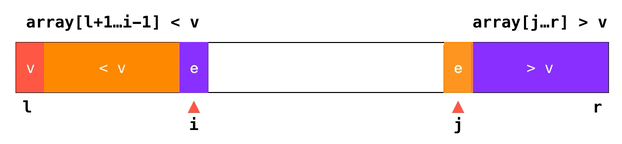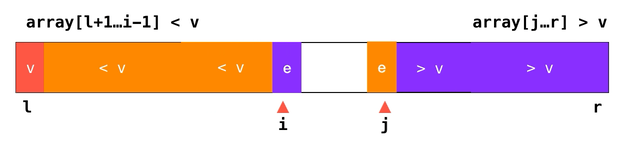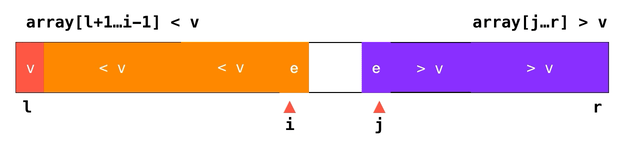
事实上上图并不准确，由于下标 i 和 j 所指代的元素 e 分别是 ≥ v 和 ≤ v 的，所以其实这样划分是将数组分为了 array[l+1...i-1] ≤ v 和 array[j...r] ≥ v 的两部分。由于存在相等元素也要交换位置的操作，所以并不会出现划分过于不平均的问题，也就避免了算法退化到这种灾难级的复杂度。这样的快速排序又称为双路快速排序。

// 双路快速排序的 partition
// 返回 p, 使得 arr[l...p-1] < arr[p]; arr[p+1...r] > arr[p]
function partition (array, l, r, cb) {
  const k = Math.floor(Math.random() * (r - l + 1) + l)
  ;[array[l], array[k]] = [array[k], array[l]]
  const v = array[l]

  // arr[l+1...i) <= v; arr(j...r] >= v
  let i = l + 1
  let j = r

  while (true) {
    // 注意这里的边界, arr[i] < v, 不能是 arr[i] <= v
    while (i <= r && cb(array[i], v)) {
      i++
    }
    // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
    while (j >= l + 1 && cb(v, array[j])) {
      j--
    }
    if (i > j) {
      break
    }
    [array[i], array[j]] = [array[j], array[i]]
    i++
    j--
  }
  [array[l], array[j]] = [array[j], array[l]]
  return j
}

示例代码 src/03-Sorting-Advance/07-Quick-Sort-Deal-With-Identical-Keys.js

三路快排 (Quick Sort 3 Ways)

简单来说，三路快排的划分操作可以表述为：

遍历数组。记小于基准 v 的部分末尾下标为 lt，大于 v 的部分首位元素为 gt，当前访问元素下标为 i，如果 i 所指元素： a. 小于 v，则与 lt+1 所指元素交换位置，同时使 lt++； b. 大于 v，则与 gt-1 所指元素交换位置，同时使 gt--； c. 等于 v则继续；

重复直到 i == gt。

// 递归的三路快速排序处理 arr[l...r]
// 将 arr[l...r] 分为 <v; == v; >v 三部分
// 之后地归对 <v; >v 两部分继续进行三路快排
// 三路排序不再简单的返回划分结果了，所以直接在排序部分遍历数组
function quickSort (array, l, r, cb) {
  // 对于小规模数组, 使用插入排序进行优化
  if (r - l <= 15) {
    insertSortPartial(array, l, r, cb)
    return
  }
  // partition
  // 随机在 arr[l...r] 的范围中, 选择一个数值作为标定点 pivot
  const k = Math.floor(Math.random() * (r - l + 1) + l)
  ;[array[l], array[k]] = [array[k], array[l]]
  const v = array[l]

  let lt = l // arr[l+1...lt] < v
  let gt = r + 1 // arr[gt...r] > v
  let i = l + 1 // arr[lt+1...i] == v
  while (i < gt) {
    if (cb(array[i], v)) {
      [array[i], array[lt + 1]] = [array[lt + 1], array[i]]
      lt++
      i++
    } else if (cb(v, array[i])) {
      [array[i], array[gt - 1]] = [array[gt - 1], array[i]]
      gt--
    } else { // arr[i] == v
      i++
    }
  }
  [array[l], array[lt]] = [array[lt], array[l]]

  quickSort(array, l, lt - 1, cb)
  quickSort(array, gt, r, cb)
}

示例代码 src/03-Sorting-Advance/08-Quick-Sort-Three-Ways.js

小结

在本小节中我为大家用相当大的篇幅介绍了快速排序，由此可见快速排序在现代算法中的重要性。

从归并排序到快速排序，我们不仅可以看到不同算法算法间巨大的差距，同时也能看到算法自身的近乎历程。快速排序就是在这样一个不断解决问题、改进自身的过程中逐步走向应用最广的排序算法的宝座的。

归并排序和快速排序他们蕴含的思想同样也为求解其他一些问题提供了思路。例如求数组中逆序对的个数，暴力解法通过考察每一对数对，显然算法复杂度为，而使用归并排序的思想逐级划分，最后算法的复杂度降低到了这样的级别；又例如去数组中第 n 大的元素，再或者简单一些：取最大、最小的元素，听起来似乎只要为数组排序就可以了，而这样算法的复杂度为，似乎已经很好了？但其实使用快速排序的思想，这个问题可以在时间里完成；那么这两个问题就给大家留作独立思考了，过段时间我会在代码仓库里共享我的解决方案，也欢迎届时一同讨论交流。

参考链接

快速排序- 维基百科，自由的百科全书