【慕课】Python 实现人工神经网络 - part.1 人工神经元

这篇文章是我在慕课网课程机器学习-实现简单神经网络是的学习笔记与老师讲课内容的整理，主要整理了算法的数学表达式部分，使用 LaTeX 进行了重新排版并通过 Katex 渲染，感兴趣并需要的同学可以查看文章的源码以获取。

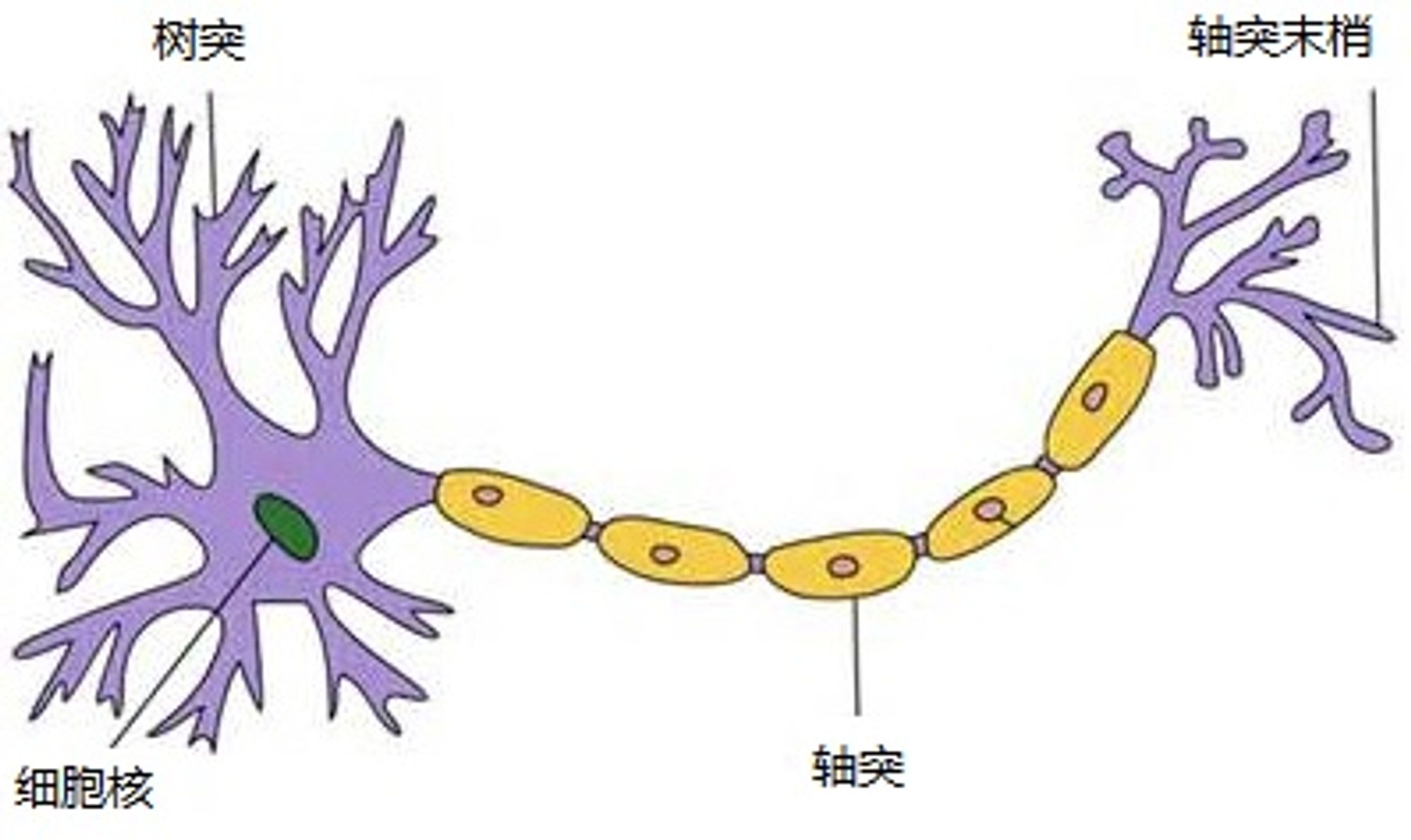
人工神经网络是一种重要的机器学习算法，其本质是实现了一种称为 "人工神经元" 的仿生学结构，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具。和其他机器学习方法一样，神经网络已经被用于解决各种各样的问题，例如机器视觉和语音识别。这些问题都是很难被传统基于规则的编程所解决的。

数学表达

激活函数

一些数学运算的概念介绍

向量点乘(内积)

例如:

矩阵转置

例如:

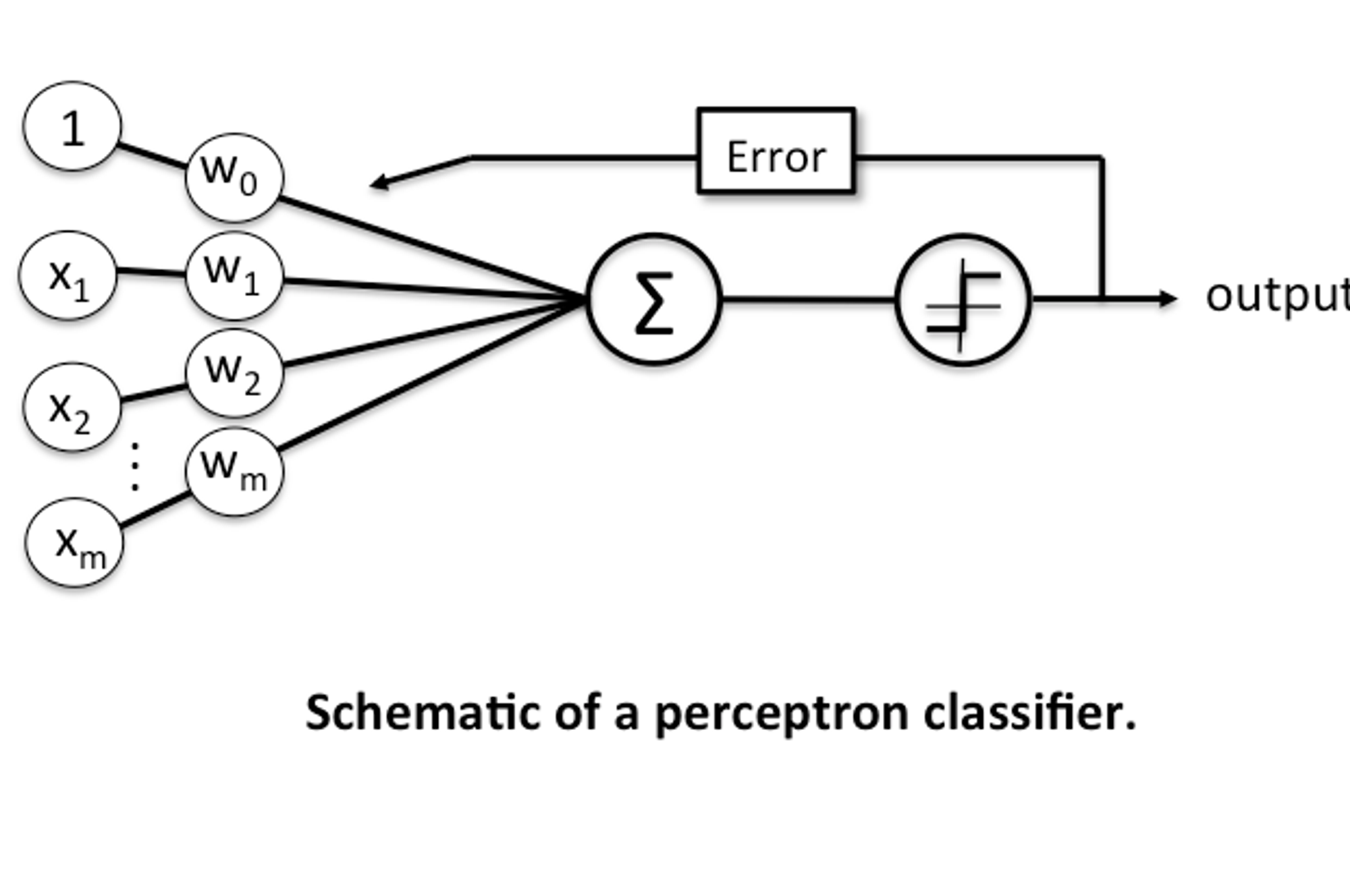
感知器数据分类算法步骤

权重向量 ，训练样本

把权重初始化为，火把每个分量初始化为间的任意小数

把训练样本输入感知器，得分类结果 ( 或 )

根据分类结果更新权重向量

步调函数（激活函数）与阈值

权重更新算法

表示学习率，是一个间的小数

是输入样本的正确分类，是感知器计算出来的分类

示例:

更新后的权重向量

阈值的更新

感知器算法适用范围

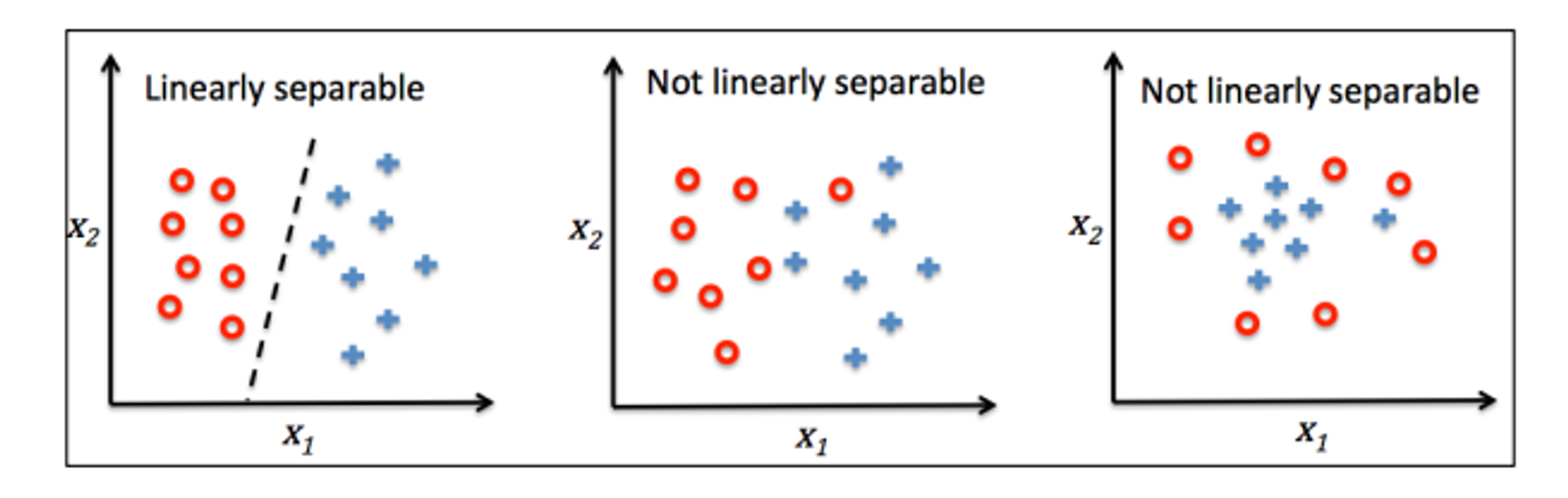
要求: 待预测的数据线性可分

算法步骤总结


import numpy as np

class Perception(object):
  """
  eta: 学习率
  n_iter: 权重向量训练次数
  w_: 神经分叉权重向量
  errors_: 用于记录神经元判断出错次数
  """
  def __init__(self, eta=0.01, n_iter=10):
    self.eta = eta;
    self.n_iter = n_iter;

  """
  X: 输入样本向量
  y: 对应样本分类
  """
  def fit(self, X, y):
    """
    输入训练数据，培训神经元

    X:shape[0_samples, n_features]
    eg: X:[[1, 2, 3], [4, 5, 6]] ===> n_samples: 2, n_features: 3

    y: [1, -1]
    """

    """
    初始化权重向量为 0
    +1: 根据算法，将 w0 设置为步调函数的初始阈值
    """
    self.w_ = np.zeros(1 + X.shape[1]);
    self.errors_ = [];

    for _ in range(self.n_iter):
      errors = 0
      """
      X:[[1,2,3], [4,5,6]]
      y:[1,-1]
      zip(X,y) = [[1,2,3, 1], [4,5,6, -1]]
      """
      for xi, target in zip(X, y):
        """
        update = η * (y - y')
        """
        update = self.eta * (target - self.predict(xi))

        """
        xi 是一个向量（数组）
        update * xi 等价于:
        [∇W(1) = X[1] * update, ∇W(2) = X[2] * update, ∇W(3) = X[3] * update]
        """
        self.w_[1:] += update * xi
        self.w_[0] += update;

        errors += int(update != 0.0)
        self.errors_.append(errors)

  def net_input(self, X):
    """
    z = w0 * 1 + w1*x1 + ... + wn*xn
    """
    return np.dot(X, self.w_[1:]) + self.w_[0]

  def predict(self, X):
    return np.where(self.net_input(X) >= 0.0 , 1, -1)

💡

数据集还是使用 Iris 数据集


file = "assets/iris.data.csv"

import pandas as pd

df = pd.read_csv(file, header=None)
df.head(10)


import matplotlib.pyplot as plt

y = df.iloc[0:100, 4].values
# print(y)
y = np.where(y == 'Iris-setosa', -1, 1)
# print(y)

X = df.iloc[0:100, [0, 2]].values

plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setasa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('花瓣长度')
plt.ylabel('花茎长度')
plt.legend(loc='upper left')
plt.show()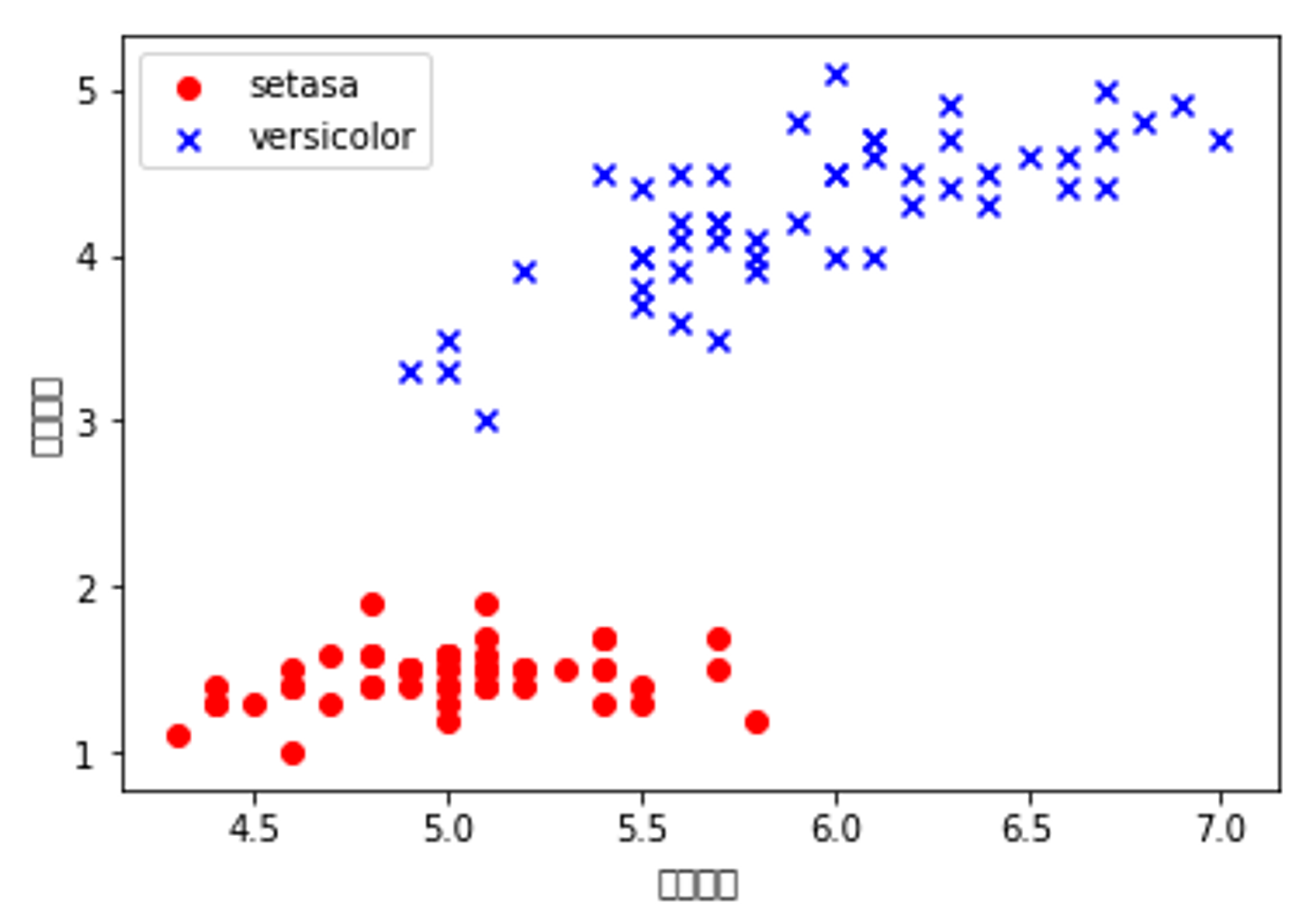


ppn = Perception(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('错误分类次数')
plt.show()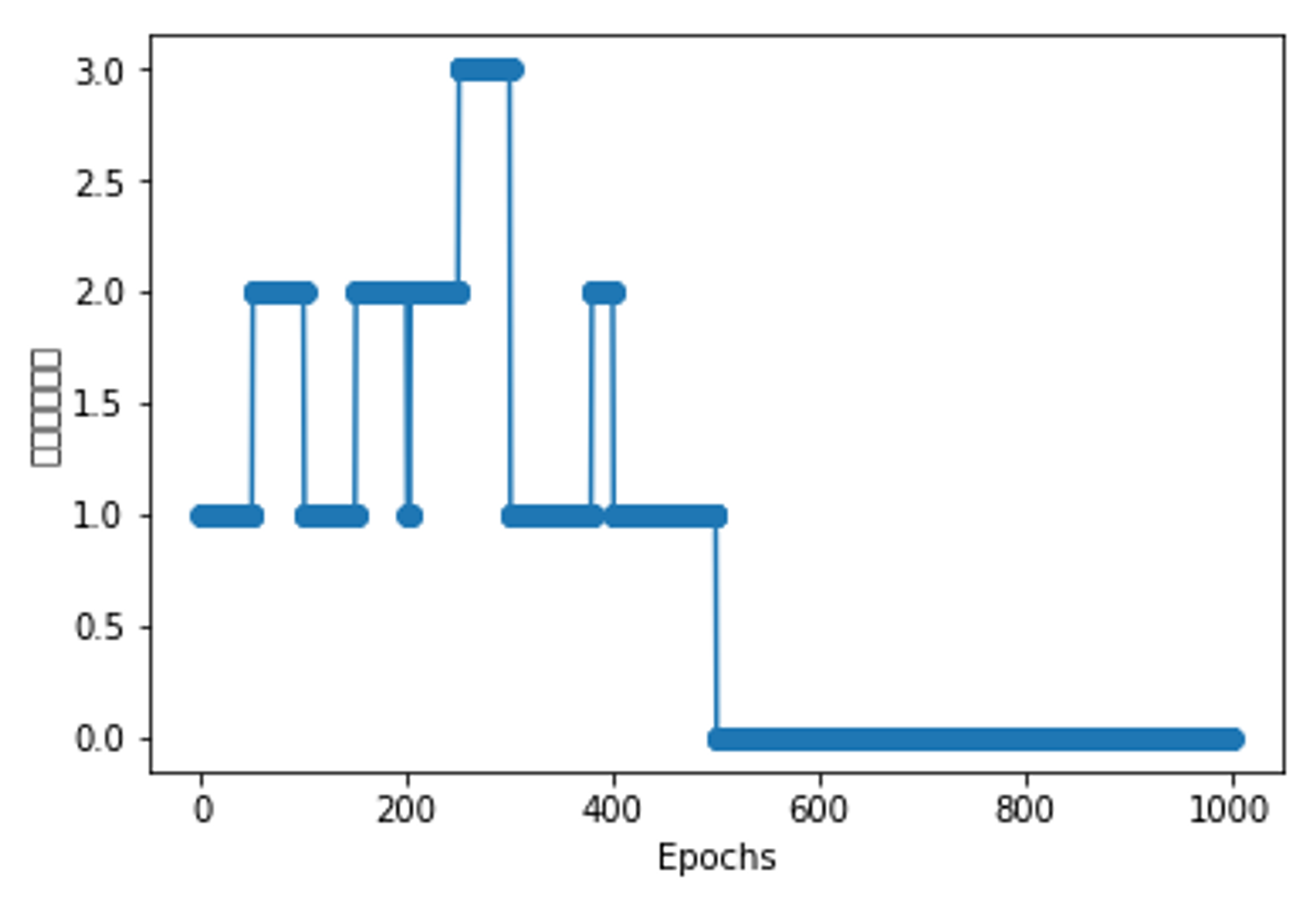


from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):
  markers = ('s', 'x', 'o', 'v')
  colors = ('red', 'blue', 'lightgreen', 'grey', 'cyan')
  cmap = ListedColormap(colors[:len(np.unique(y))])

  x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max()
  x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max()

  xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                        np.arange(x2_min, x2_max, resolution))

  z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)

  z = z.reshape(xx1.shape)
  plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)
  plt.xlim(xx1.min(), xx1.max())
  plt.ylim(xx2.min(), xx2.max())

  for idx, cl in enumerate(np.unique(y)):
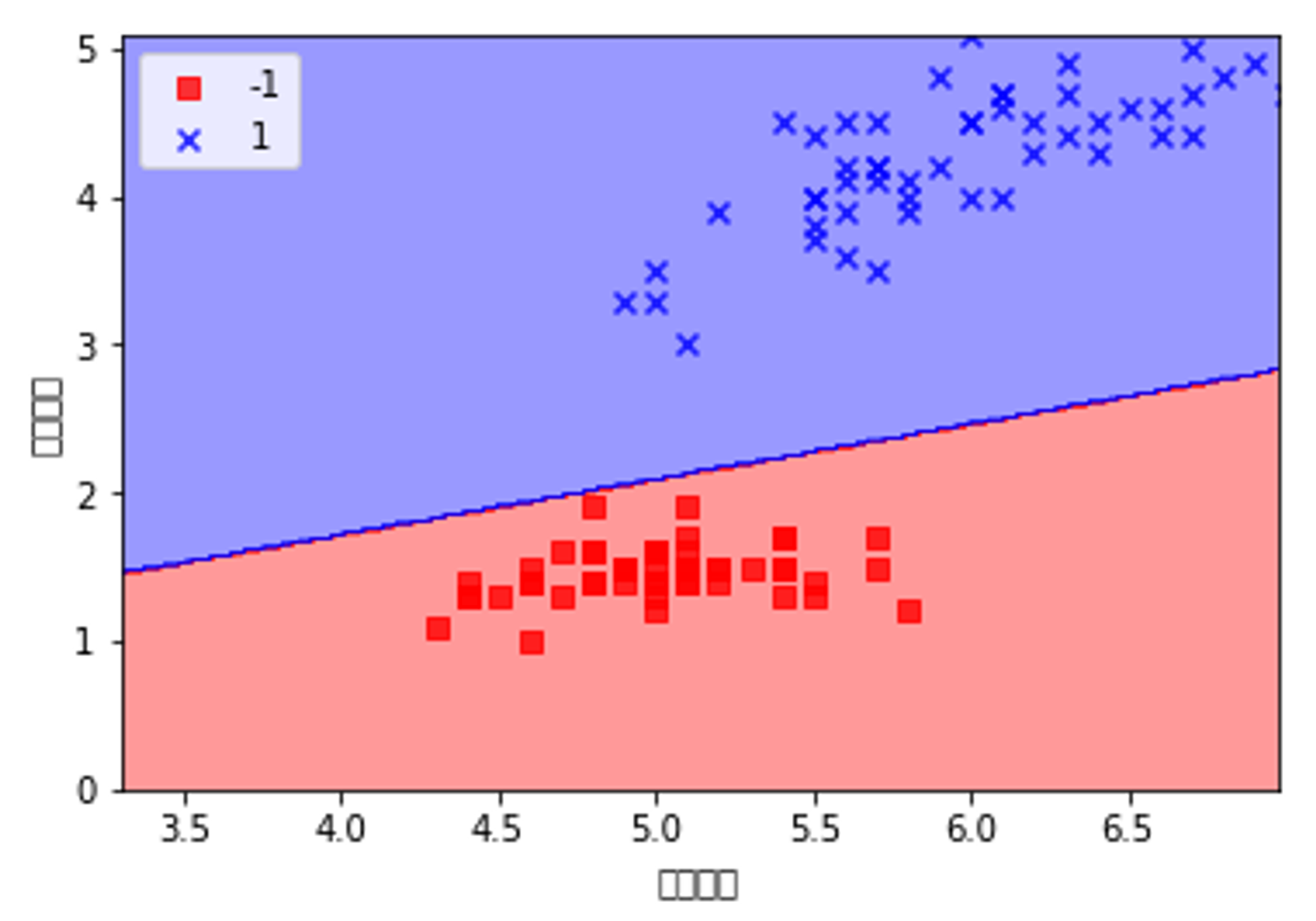
    plt.scatter(x=X[y==cl, 0], y = X[y==cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)


plot_decision_regions(X, y, ppn, resolution=0.02)
plt.xlabel('花瓣长度')
plt.ylabel('花茎长度')
plt.legend(loc='upper left')
plt.show()