K-means算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
k个初始类聚类中心点的选取对聚类结果具有较大的影响,因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心,初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象,根据其与各个簇中心的距离将每个对象重新赋给最近的簇。当考察完所有数据对象后,一次迭代运算完成,新的聚类中心被计算出来。如果在一次迭代前后,J的值没有发生变化,说明算法已经收敛。
算法步骤:
- 创建k个点作为起始支点(随机选择)
- 当任意一个簇的分配结果发生改变的时候
- 对数据集的每个数据点
- 对每个质心
- 计算质心与数据点之间的距离
- 将数据分配到距离其最近的簇
- 对每一簇,计算簇中所有点的均值并将其均值作为质心
iris
首先从
sklearn 导入数据集。我们用非常著名的 iris 数据集。from sklearn import datasets
from matplotlib import pyplot as plt
iris = datasets.load_iris()
X, y = iris.data, iris.target
data = X[:,[1,3]]# 为了便于可视化,只取两个维度
plt.scatter(data[:,0],data[:,1]);
欧式距离
计算欧式距离,我们需要为每个点找到离其最近的质心,需要用这个辅助函数。
import numpy as np
def distance(p1,p2):
"""
Return Eclud distance between two points.
p1 = np.array([0,0]), p2 = np.array([1,1]) => 1.414
"""
tmp = np.sum((p1-p2)**2)
return np.sqrt(tmp)
distance(np.array([0,0]),np.array([1,1]))
out: 1.4142135623730951
随机质心
在给定数据范围内随机产生k个簇心,作为初始的簇。随机数都在给定数据的范围之内
dmin + (dmax - dmin) * np.random.rand(k) 实现。def rand_center(data,k):
"""Generate k center within the range of data set."""
n = data.shape[1]# features
centroids = np.zeros((k,n))# init with (0,0)....for i in range(n):
dmin, dmax = np.min(data[:,i]), np.max(data[:,i])
centroids[:,i] = dmin + (dmax - dmin) * np.random.rand(k)
return centroids
centroids = rand_center(data,2)
centroids
out: array([[4.18354619, 2.3433686 ],[3.22403937, 0.17507507]])
k均值聚类
这个基本的算法只需要明白两点。
- 给定一组质心,则簇更新,所有的点被分配到离其最近的质心中。
- 给定k簇,则质心更新,所有的质心用其簇的均值替换
当簇不在有更新的时候,迭代停止。当然kmeans有个缺点,就是可能陷入局部最小值,有改进的方法,比如二分k均值,当然也可以多计算几次,去效果好的结果。
def kmeans(data,k=2):
def _distance(p1,p2):
"""
Return Eclud distance between two points.
p1 = np.array([0,0]), p2 = np.array([1,1]) => 1.414
"""
tmp = np.sum((p1-p2)**2)
return np.sqrt(tmp)
def _rand_center(data,k):
"""Generate k center within the range of data set."""
n = data.shape[1]# features
centroids = np.zeros((k,n))# init with (0,0)....for i in range(n):
dmin, dmax = np.min(data[:,i]), np.max(data[:,i])
centroids[:,i] = dmin + (dmax - dmin) * np.random.rand(k)
return centroids
def _converged(centroids1, centroids2):
# if centroids not changed, we say 'converged'
set1 = set([tuple(c) for c in centroids1])
set2 = set([tuple(c) for c in centroids2])
return (set1 == set2)
n = data.shape[0]# number of entries
centroids = _rand_center(data,k)
label = np.zeros(n,dtype=np.int)# track the nearest centroid
assement = np.zeros(n)# for the assement of our model
converged = False
while not converged:
old_centroids = np.copy(centroids)
for i in range(n):
# determine the nearest centroid and track it with label
min_dist, min_index = np.inf, -1
for j in range(k):
dist = _distance(data[i],centroids[j])
if dist < min_dist:
min_dist, min_index = dist, j
label[i] = j
assement[i] = _distance(data[i],centroids[label[i]])**2
# update centroidfor m in range(k):
centroids[m] = np.mean(data[label==m],axis=0)
converged = _converged(old_centroids,centroids)
return centroids, label, np.sum(assement)
由于算法可能局部收敛的问题,随机多运行几次,取最优值
best_assement = np.inf
best_centroids = None
best_label = None
for i in range(10):
centroids, label, assement = kmeans(data,2)
if assement < best_assement:
best_assement = assement
best_centroids = centroids
best_label = label
data0 = data[best_label==0]
data1 = data[best_label==1]
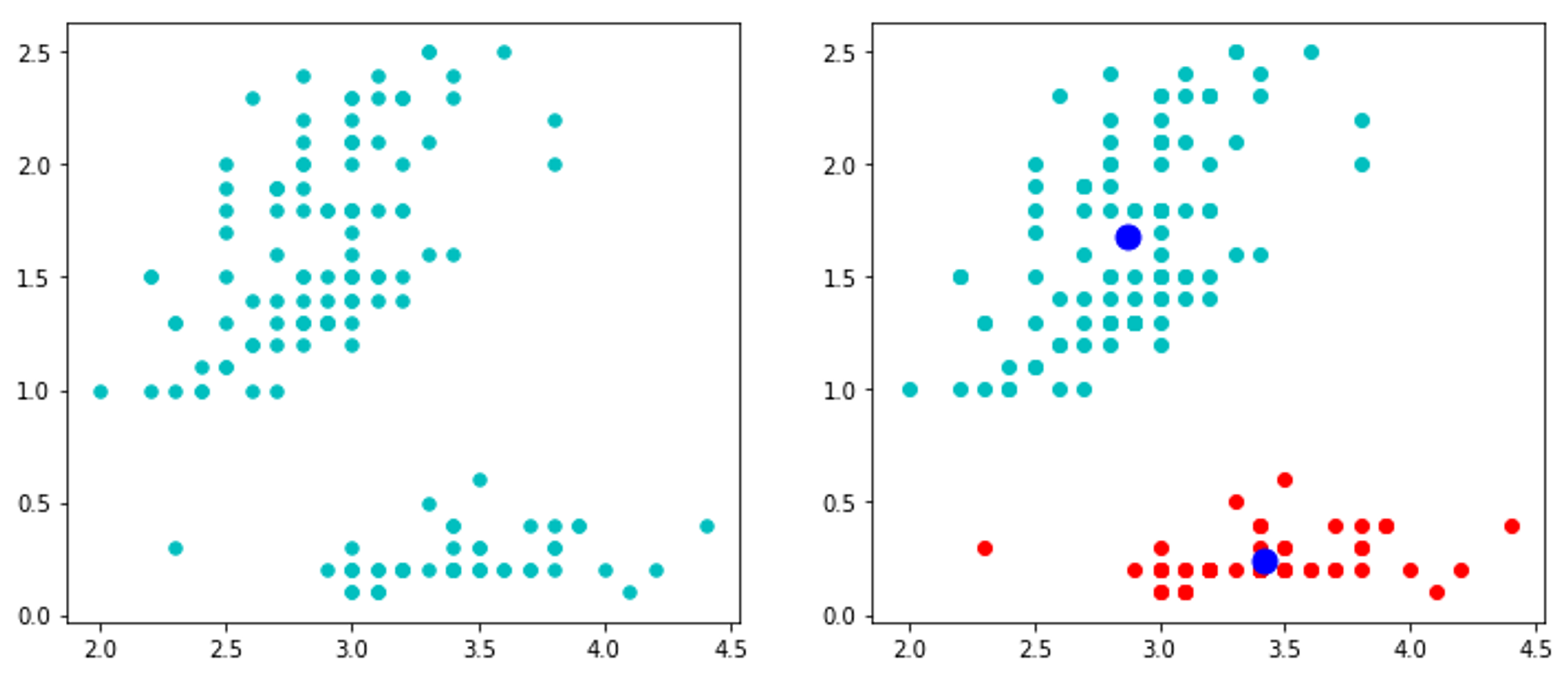
如下图,我们把数据分为两簇,绿色的点是每个簇的质心。
fig, (ax1,ax2) = plt.subplots(1,2,figsize=(12,5))
ax1.scatter(data[:,0],data[:,1],c='c',s=30,marker='o')
ax2.scatter(data0[:,0],data0[:,1],c='r')
ax2.scatter(data1[:,0],data1[:,1],c='c')
ax2.scatter(centroids[:,0],centroids[:,1],c='b',s=120,marker='o')
plt.show()