这篇文章是我在慕课网课程 机器学习-实现简单神经网络 是的学习笔记与老师讲课内容的整理，主要整理了算法的数学表达式部分，使用 LaTeX 进行了重新排版并通过 Katex 渲染，感兴趣并需要的同学可以查看文章的源码以获取

距离的定义

• 和方差公式

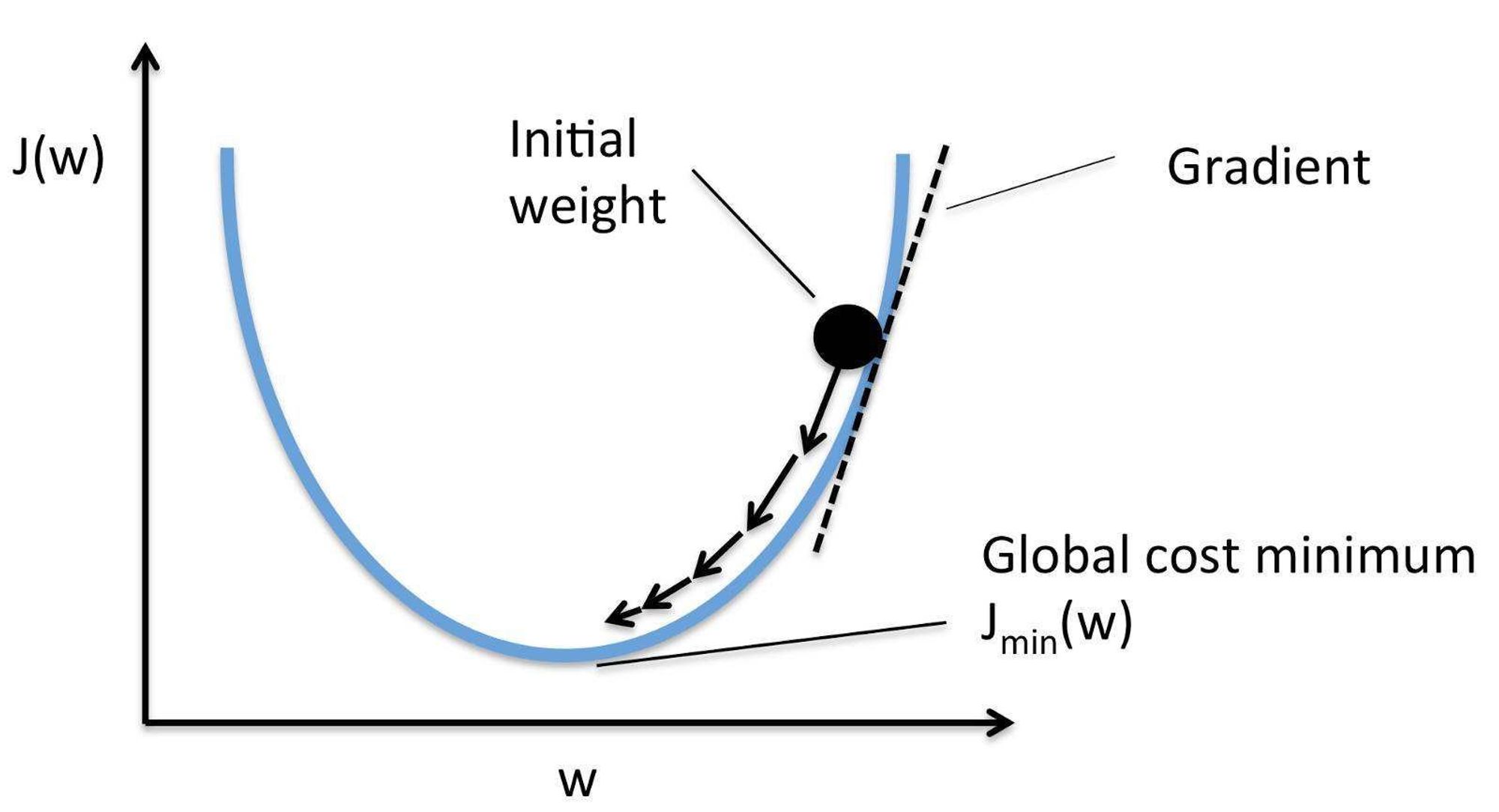
渐进下降法 (梯度下降)

和方差求偏导数

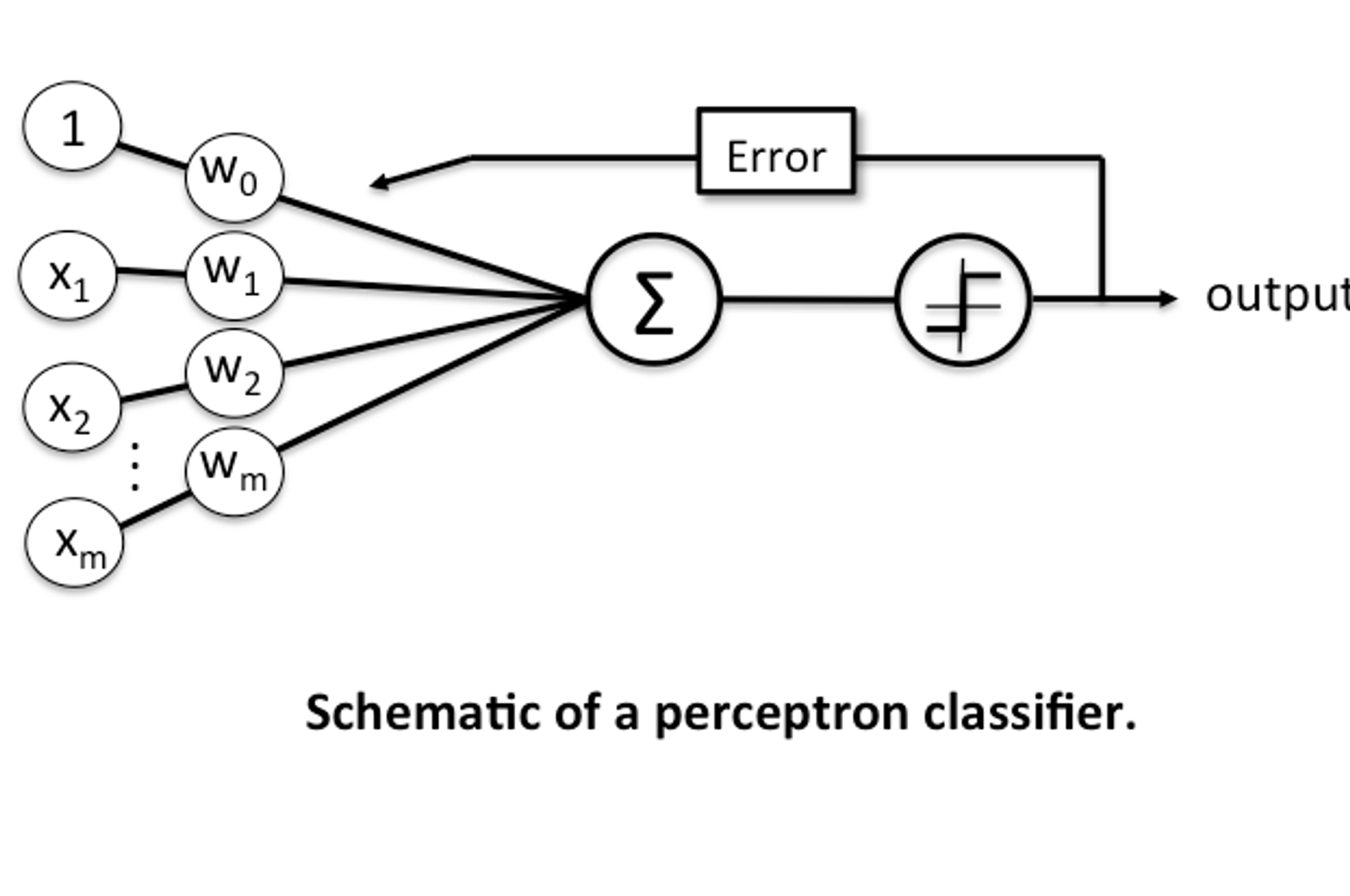
神经元参数更新

class AdalineGD(object):
  """
  eta: float
  学习效率，[0, 1]

  n_iter: int
  对训练数据进行学习改新的次数

  w_: 一维向量
  存储权重数值

  error_: 一维向量
  存储每次迭代改进是，网络对数据进行错误判断的次数
  """
  def __init__(self, eta=0.01, n_iter=50):
    self.eta = eta
    self.n_iter = n_iter

  def fit(self, X, y):
    """
    X: 二维数组 [n_sampls, n_features]
    n_smapls 表示 X 中含有训练数据条目数
    n_features 含有 4 个数据的一维向量，用于表示一条训练条目

    y: 一维向量
    用于存储每一条训练条目对应的正确分类
    """
    self.w_ = np.zeros(1 + X.shape[1])
    self.cost_ = []

    for i in range(self.n_iter):
      output = self.net_input(X)
      errors = (y - output)
      self.w_[1:] += self.eta * X.T.dot(errors)
      self.w_[0] += self.eta * errors.sum()
      cost = (errors ** 2).sum() / 2.0
      self.cost_.append(cost)

  def net_input(self, X):
    return np.dot(X, self.w_[1:]) + self.w_[0]

  def activation(self,X):
    return self.net_input(X)

  def predict(self, X):
    return np.where(self.activation(X) >= 0, 1, -1)

ada = AdalineGD(eta=0.0001, n_iter=50)
ada.fit(X, y)

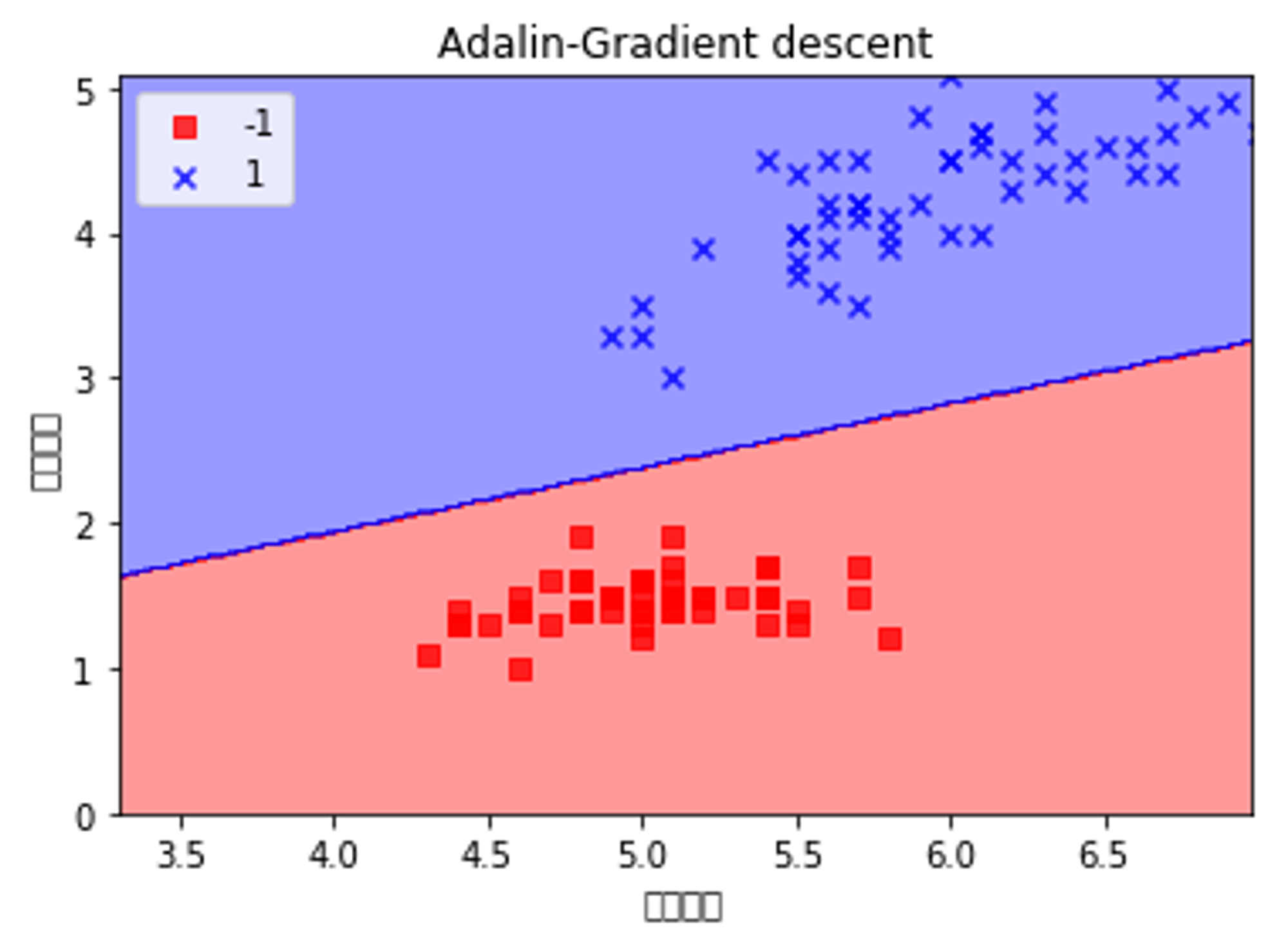
plot_decision_regions(X, y, classifier=ada)
plt.title('Adalin-Gradient descent')
plt.xlabel('花径长度')
plt.ylabel('花瓣长度')
plt.legend(loc='upper left')
plt.show()

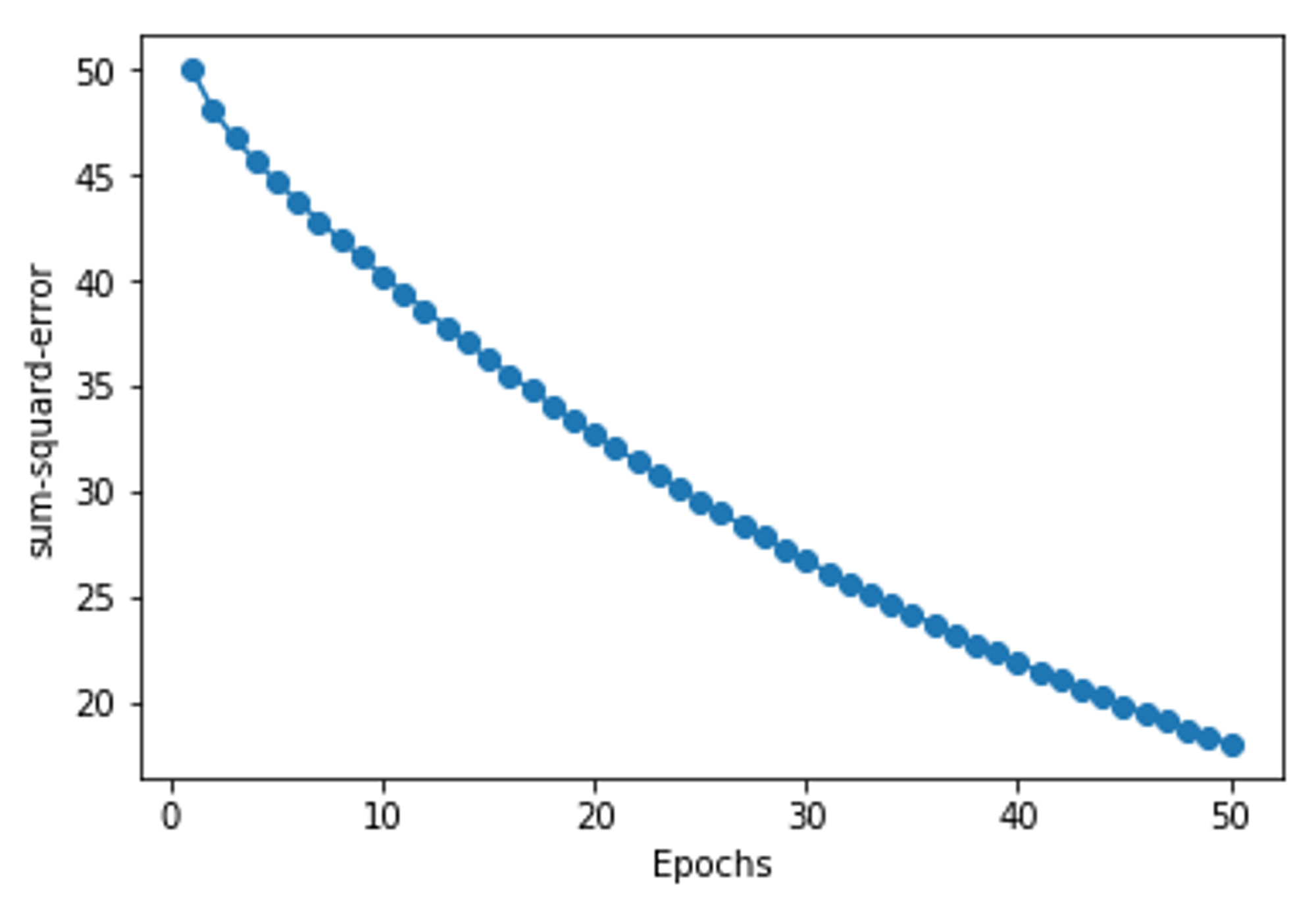
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('sum-squard-error')
plt.show()