【慕课】重学算法 - part.4 二分搜索树 (3)

这系列文章是慕课网《算法与数据结构》实战课程老师的讲授内容笔记整理，其中有很多动图都是我参考老师的动画演示自己制作的，并提供 JS(es6) 版的代码示例。代码仓库：📦 https://github.com/Mitscherlich/Play-with-Algorithms-JS

删除元素

接下来我们要面对的是二分搜索树中最困难的操作：删除一个元素。事实上，我们找到一个元素很容易，直接将它删除也不难，但关键是如何在删除一个元素之后，通过对左右子树的一系列操作，继续维持二分搜索树的性质。为了解决这个问题，我们从特殊到一般两种不同的情况入手。

最小值和最大值

得利于二分搜索树的定义，我们很容易就能通过递归的方式编写出查找最大最小节点的算法。简单来说，如果查找最大值，只需从根结点起，逐级遍历它的右子树，直到没有右孩子的节点；反之，如果查找最小值，则只需要向左子树中递归搜索即可。

/**
 * 在以 node 为根的二叉搜索树中返回最小键值的节点
 * @param {Node} node 待搜索二分搜索树的根节点
 * @return {Node} 最小值节点
 */
function minimum (node) {
  if (node.left === null) {
    return node
  }
  return minimum(node.left)
}

/**
 * 在以 node 为根的二叉搜索树中返回最大键值的节点
 * @param {Node} node 待搜索二分搜索树的根节点
 * @return {Node} 最大值节点
 */
function maximum (node) {
  if (node.right === null) {
    return node
  }
  return maximum(node.right)
}

示例代码 src/05-Binary-Search-Tree/07-Binary-Search-Tree-Remove-Min-and-Max.js

要删除找出来的元素，还需要考虑特殊情况：如果最小(大)的元素正好是叶子结点(没有左右孩子)，这是直接删除掉这个节点就可以了；

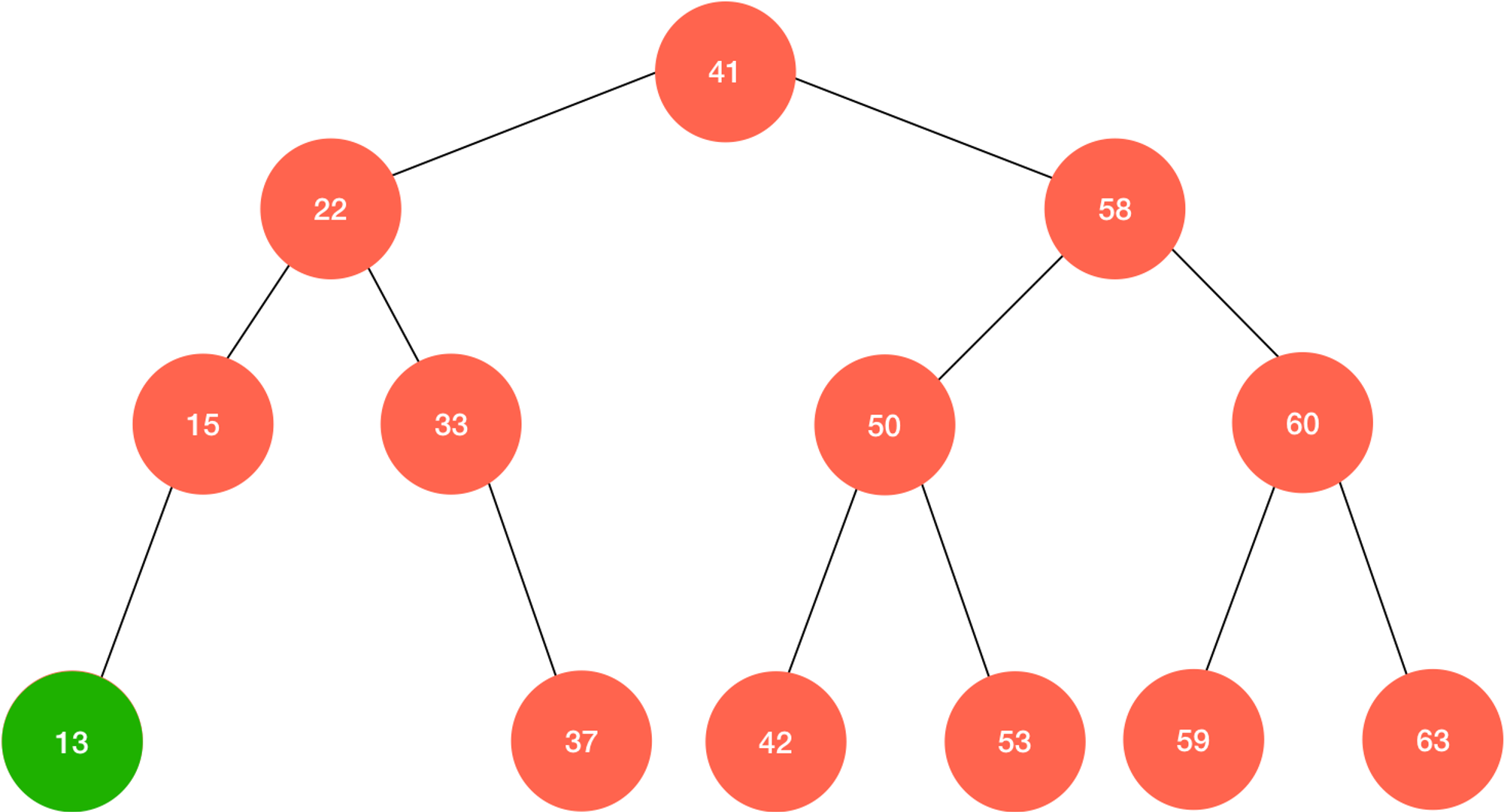
如果最小元素有右孩子(或最大元素有右孩子)，这时也不难看出，此时待删除节点的右子树(左子树)的根节点正好就是比它的父节点更小(大)那么一点的元素，这说明只需要将这颗子树的根结点替换掉原来的节点即可：

/**
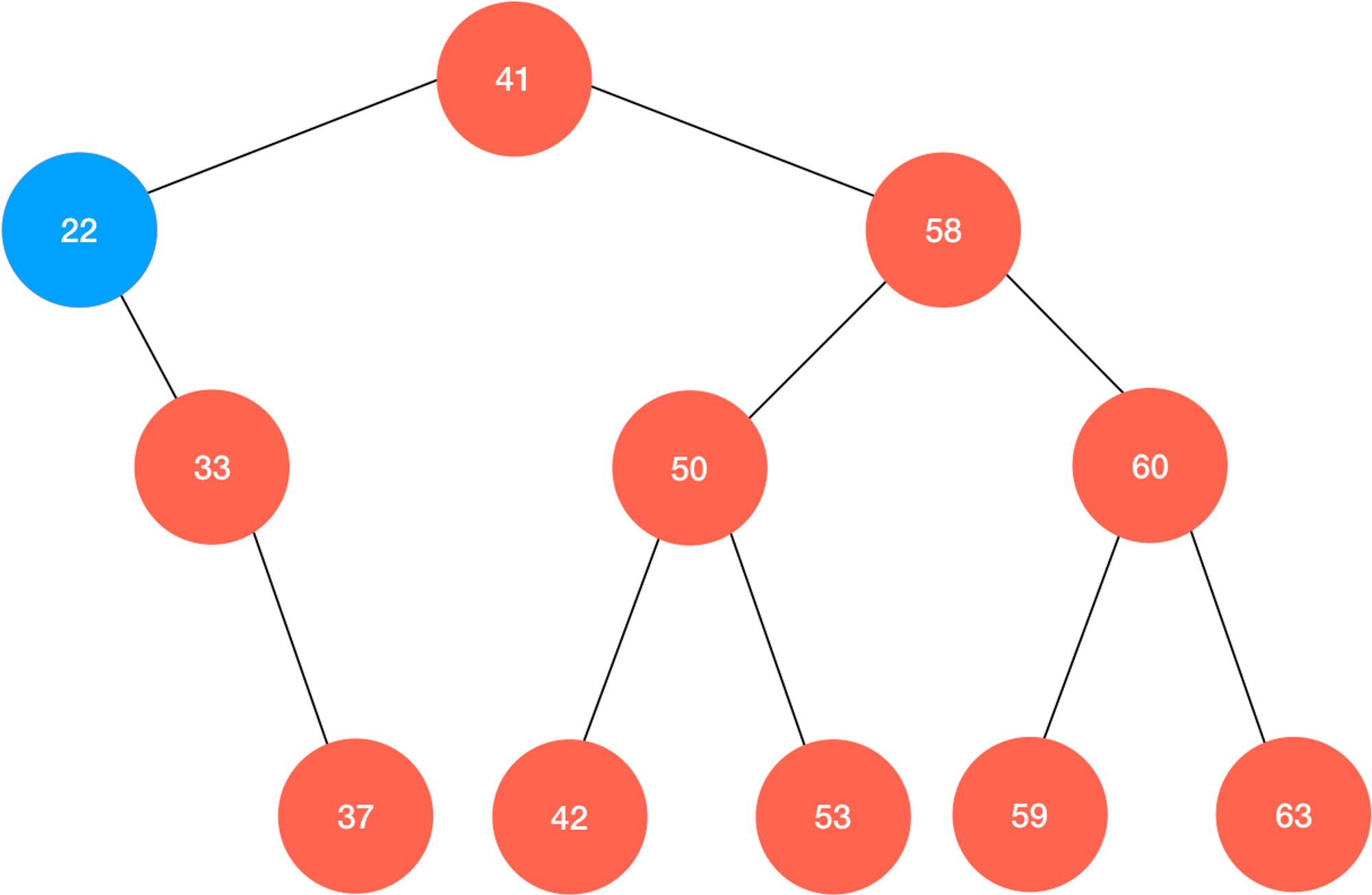
 * 删除掉以 node 为根的二分搜索树中的最小节点
 * @param {Node} node 待搜索二分搜索树的根节点
 * @return {Node|null} 新的二分搜索树的根
 */
function removeMin (node) {
  if (node.left === null) {
    return node.right
  }
  node.left = removeMin(node.left)
  return node
}

/**
 * 删除掉以 node 为根的二分搜索树中的最大节点
 * @param {Node} node 待搜索二分搜索树的根节点
 * @return {Node|null} 新的二分搜索树的根
 */
function removeMax (node) {
  if (node.right === null) {
    return node.left
  }
  node.right = removeMax(node.right)
  return node
}

class BinarySearchTree {
  ...
  /**
   * 从二分搜索树中删除最小值所在的节点
   */
  removeMin() {
    if (this.root) {
      this.root = removeMin(this.root)
      this.count -= 1
    }
  }
  /**
   * 从二分搜索树中删除最大值所在的节点
   */
  removeMax () {
    if (this.root) {
      this.root = removeMax(this.root)
      this.count -= 1
    }
  }
}

我们从上面的代码中不难发现，删除最小值(或最大值)所在的节点无外乎就是删除有 0 个或 1 个子树的节点，也就意味着这样的算法其实对任意只有一个子树的节点都是成立的：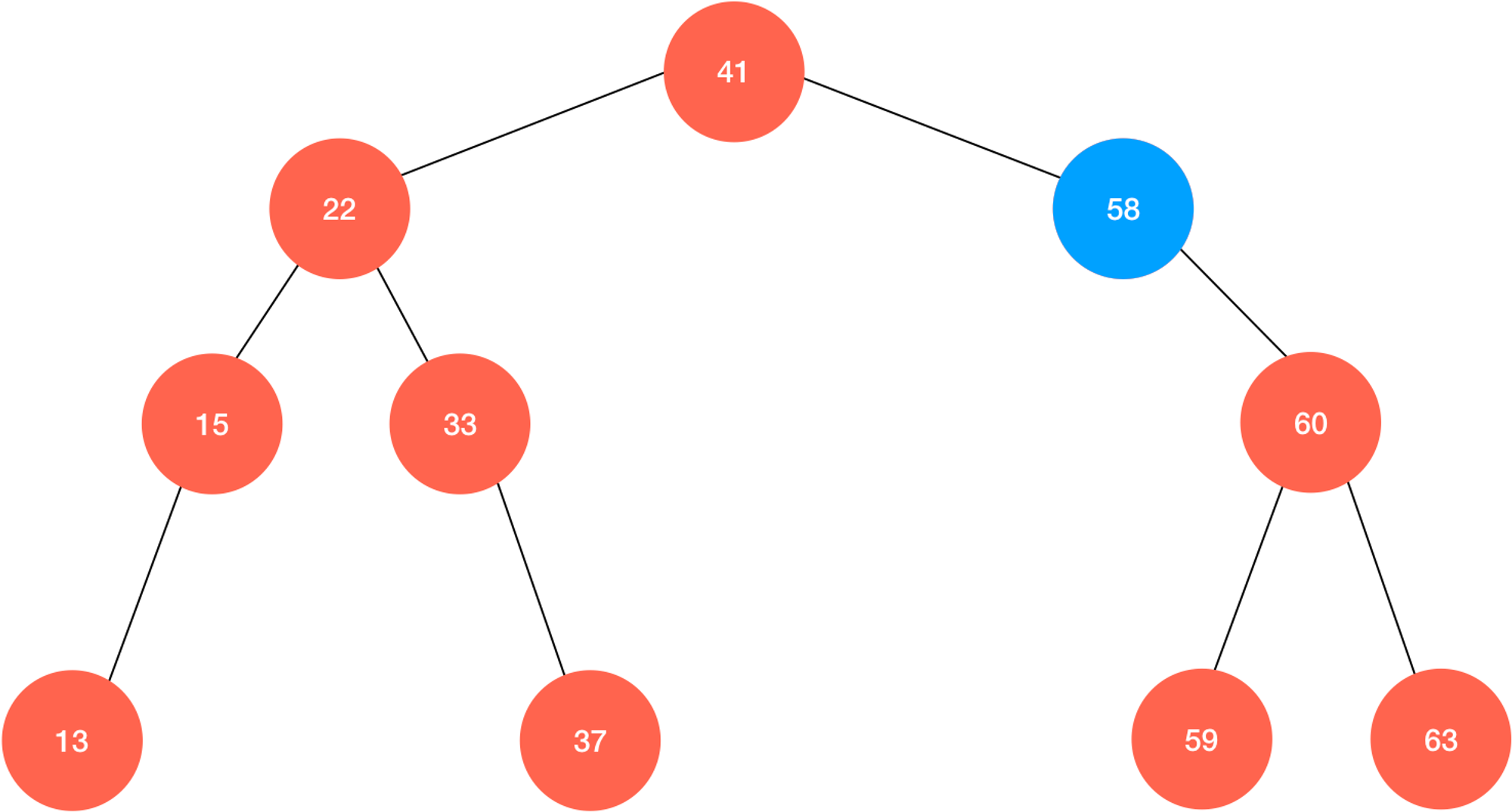

任意元素

为了解决删除二分搜索树中的任意元素的问题，我们还需要一个更通用的算法。一个相当经典的算法由 Hibbard 于 1962 年提出(又称为 Hibbard Deletion)。

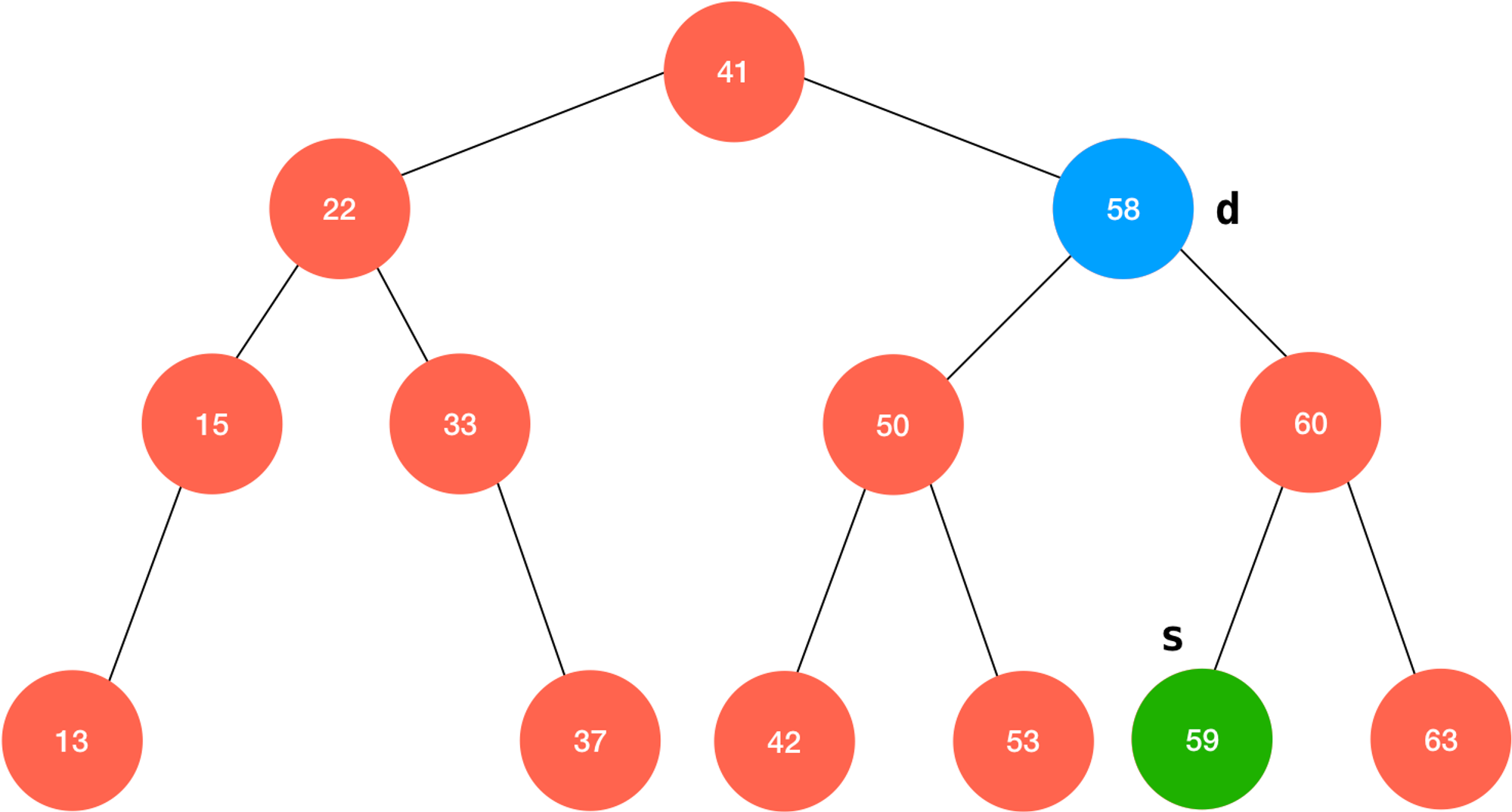
Hibbard Deletion 的核心思想和之前的特殊情况一样，都是为要删除的节点找到一个合适的替代元素，而 Hibbard Deletion 指出这个要删除的节点的后继 (successor) 正是那个合适的元素，即右子树中的最小值；简单来说，应用 Hibbard Deletion 删除一个元素 d 的算法流程为：

找到 d 的后继 s: s = minimun(d.right);

将 s 从 d 的右子树中移除: s.right = removeMin(d.right);

删除 d, s 是新的子树的根: s.left = d.left。

动画演示:

/**
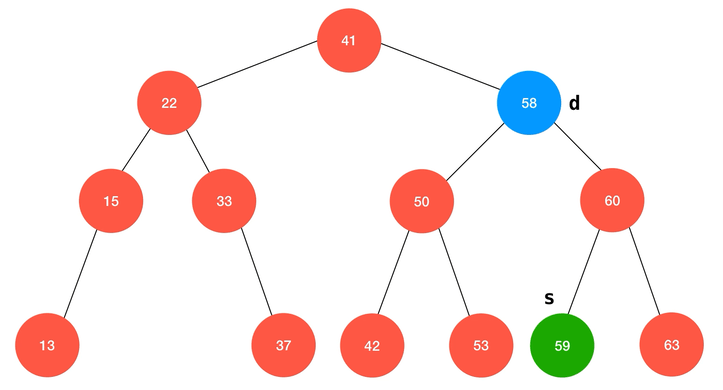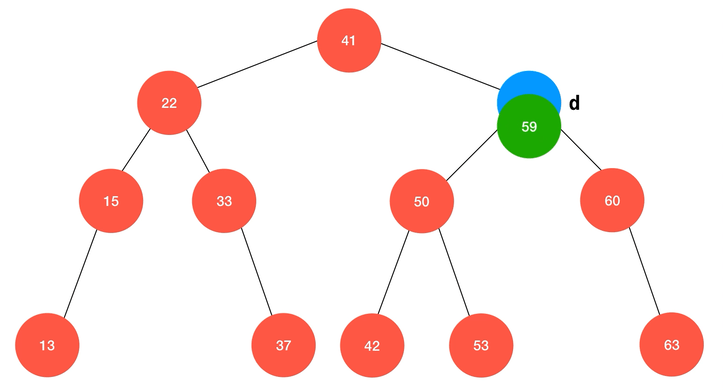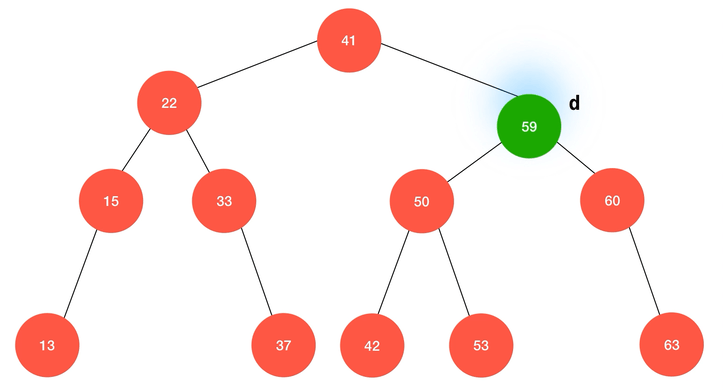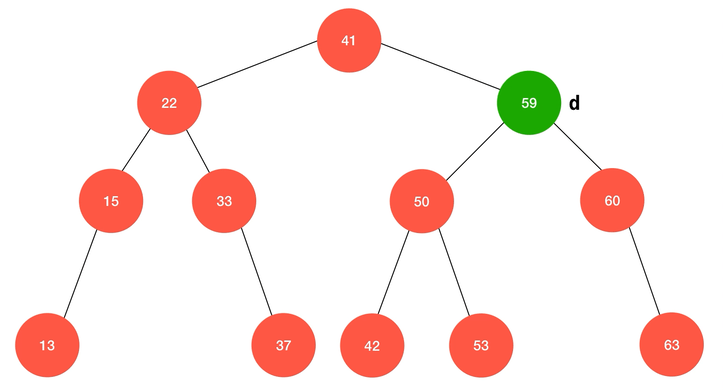
 * 删除掉以 node 为根的二分搜索树中间键值为 key 的节点
 * @param {Node} node 以 node 为根的二分搜索树
 * @param {*} key 待删除的键值
 * @return {Node} 返回删除节点后新的二分搜索树的根
 */
function remove (node, key) {
  if (node === null) {
    return null
  }
  if (key < node.key) {
    node.left = remove(node.left, key)
    return node
  } else if (key > node.key) {
    node.right = remove(node.right, key)
    return node
  } else { // k == node.key
    if (node.left === null) {
      return node.right
    }
    if (node.right === null) {
      return node.left
    }
    // node.left !== null && node.right !== null
    const successor = new Node(minimum(node.right))
    successor.right = removeMin(node.right)
    successor.left = node.left
    return successor
  }
}

class BinarySearchTree {
  ...
  /**
   * 删除任意元素
   * @param {*} k 待删除的键值
   */
  remove (k) {
    if (this.root) {
      this.root = remove(this.root, k)
      this.count -= 1
    }
  }
}

类似的，一个合理的变形是 Hibbard Deletion 的替代节点也可以是带删除节点的前驱 (predecessor)，即左子树中的最大值；我们也很容易改写算法流程：

找到 d 的前驱 p: p = maximum(d.right);

将 p 从 d 的左子树中移除: p.left = removeMax(d.left);

删除 d, p 是新的子树的根: p.right = d.right。

感兴趣的读者可以自己编写一个这样的 Hibbard Deletion，效果应该是一样的。

小结

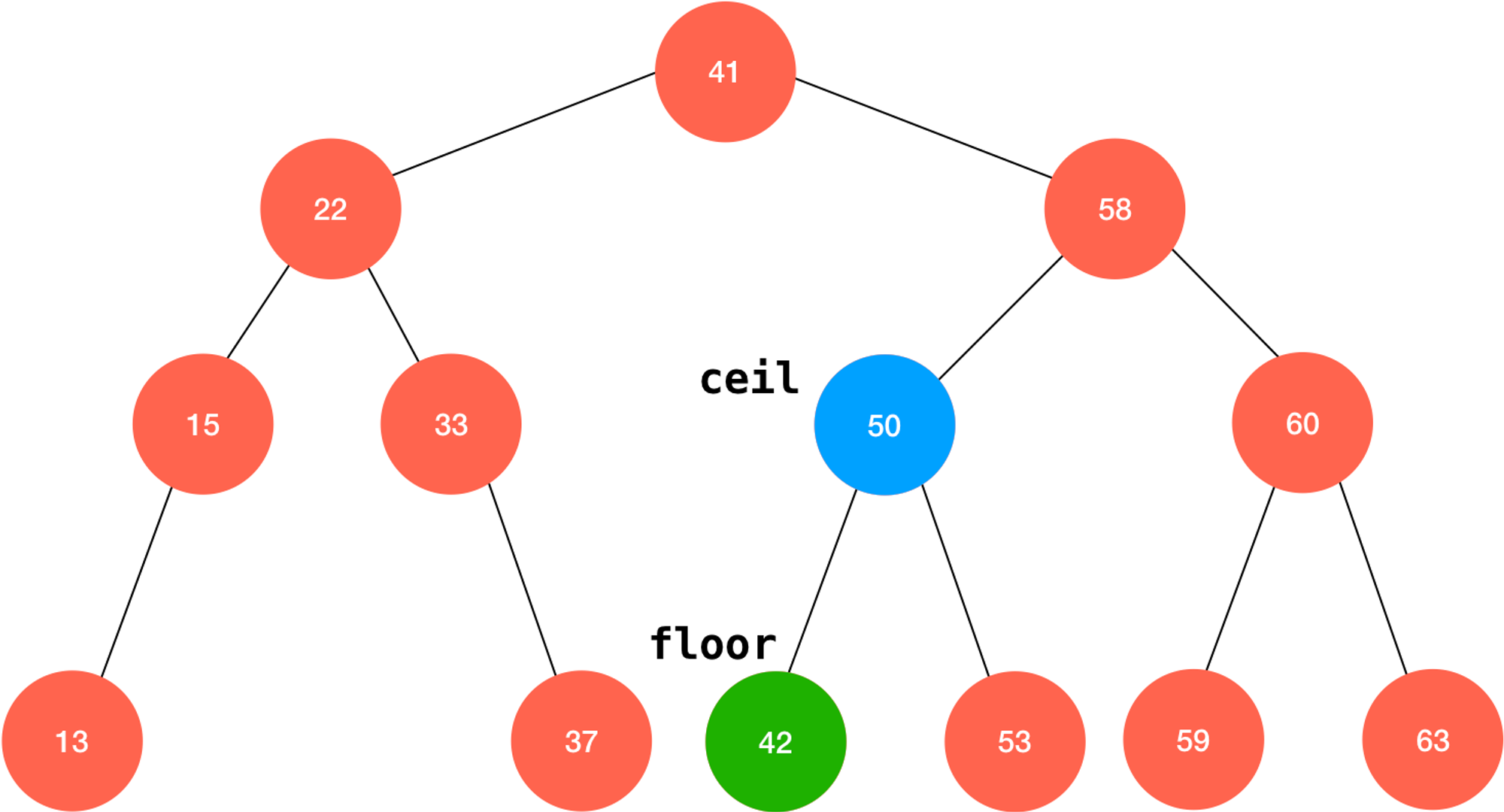
在这一章中我们详细学习了二分搜索树这种数据结构以及它的相关操作。事实上这还只是二分搜索树应用中的一部分，二分搜索树还具有很多优秀的性质使得它可以回答很多数据之间的关系，例如我们已经实现的查找最大、最小值、找到一个元素的前驱和后继等，类似的我们还可以实现之前在二分搜索法中提到的 floor 和 ceil 操作：

示例代码 src/05-Binary-Search-Tree/Opt-Floor-and-Ceil-in-BST.js

💡

不一定所有的元素的 floor 和 ceil 都是它自身，例如图中 43 的 floor 就是它的前驱 42，ceil 就是它的后继 50；再者也不是所有的元素都有 floor 和 ceil，例如 11 就只有 ceil 13 而没有 floor —— 它比最小的元素还要小

类似的，二分搜索树还支持回答 rank 或者 selection 这样的问题：rank 是回答一个元素在二分搜索树中的排名，而 selection 则是获取排名第 n 位的元素。再比如，还可以通过一些改造，使得现有的二分搜索树支持重复的元素。限于篇幅原因这里就不一一展开细说了，感兴趣的同学不妨作为练习来实现一下这些功能。

参考链接

二叉搜索树 - 维基百科